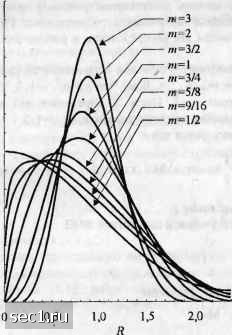Рис. 2.1.10. Графики ФПВ для «/-распределения при П=1.

т - параметр згшираний. (Mijagakinxip., 1978)

Это важное свойство га) ccobcivH.4 случайны.х величин, которое, вообще говоря, не выполняется ди други.\ распределений. Оно распространяется на «-мерные гауссовские случайные величины непосредственно. Это означает, что если pj,=0 при ij, то случайные велганы Х„ i= /=1, 2,... я являются некоррелированными и, следовательно, статистически

независимыми.

Теперь рассмотрим линейные преобразования п гауссовых случайных величин Х„ 1= /=1, 2, ... с вектором средних ш,. и ковариационной матрицей М.

Пусть

Y=AX, (2.1.157)

где А - невырожденная матрица. Как показано раньше, якобиан этого преобразования J = 1/det А. Подстав.л5ш

X=A"Y в (2.1.150), no.Tj-iHM СФПВ для Y в виде

Р(У) =

(2я) 1

(detM)*MetA

exp[-A(A-y-niJM-4A-y-mJ] =

(2я)" 2(detQ)

-fyexp[-(y-m,)Q Чу-Шу)].

(2.1.158)

где вектор т, и матрица Q определяются так

m =Ат

(2.1.159)

Q = AMA.

Таким образом, мы показали, что линейное преобразование ряда совместно гауссовских случайных велишн приведёт к другому ряду также совместно гауссовских величин.

Предположим, что мы хотим с помощью линейных преобр.130ваний перейти к п статистически нез;1висимым случайным величинам. Как выбрать в этом случае матрицу А? Из предыдущего обсуждения мы знаем, что гауссовс1сие случайные величины статистически независимы, если они попарно не коррелированы, т.е. если ковариационная матрица Q является диагональной. Следовательно, мы должны потребов;1ть

AMA=D, (2.1.1Г.0)

где D - диагональная матрица. Матрица М - это ковариационная матрица, следовательно, она положительно определённая. Одно решение (2.1.160) сводится к выбору ортогональной матрицы А (А=А"), состоящей из столбцов, которые являются собственными векторами ковариационной матрицы М. Тогда D является диагональной матрицей с диагональными элементами, равными собственным векторам ковариационной матрицы М.

Пример 2.1.5. Рассмотрим двухмерную гауссовскую ФПВ с ковариационной матрицей

1 " 1/2

1/2 1

Определим преобразование А, которое приводит к некоррелированным случайным велшнам. Сначала решим задачу о собственных значениях М. Характеристическое уравнение, которое их определяет,

det (М.-ХТ)=0, (1-)-1/4=0, Х=3/2, 1/2.

Далее мы определим два собственных вектора. Если а означает собственный вектор, имеем уравнение

(М-;\.1)а=0.

При Xi=3/2 и Хл=1/2 мы поялчаем собственные векторы

Hi =

Следовательно,

1 1

1 -1

Л = л(

Легко поюоать. что А"=А и АМА=В, где диагошьльные элементы D равны 3/2 и 1/2. 2.1.5. Верхняя граница для вероятностей «хвостов»

При определении характеристик систем цифровой связи часто необходимо определить площадь, ограниченную хвостами ФПВ Мы назовём эту площадь вероятностью хвостов. В этом разделе мы представим две верхние границы для вероятности хвостов.

Первая, полученная из неравенства Чебышева, до некоторой степени грубая. Вторая, называемая границей Чернова, более плотная.

Неравенство Чебышева. Допустим, что Х- произвольная случайная величина с ограниченным средним значением т у, и ограниченной дисперсией а. Для произвольного положительного числа 5

Р(Х-т 5)<

(2.1.161)

Это соотношение называется неравенством Чебышева. Доказательство этой границы относительно простое. Имеем

o:=f {x-mj- p{x)dx> j(x-mjp(x)dx>5- p(x)dx 5P(\X - т.\>Ь). Таким образом, справедливость неравенства установлена.

Очевидно, что неравенство Чебышева непосредственно даёт верхнюю границу площади, ограниченной хвостами ФПВ р(у), где Y=X-m.r, те для площади под р(у) в интервале (-<»,-5) и (5,оо). Следовательно, неравенство Чебышева можно выразить в виде

l-[F,(5)-F,(-5)]<t

или эквивалентным образом:

l-[F,(/«,.+5)-F,(m,-5)]<.

(2.1.162)

(2 1.163)

На границу Чебышева можно посмотреть с другой точки зрения. Используя случайную величину с нулевым средним У=Х-ту, для удобства определим функцию g(Y) в виде

Поскольку функция g(Y) равна О или 1 с вероятностью соответственно Р[У<5] и Р[]>5], её среднее значение

E[giY)]-P(}}]>5) (2.1.165)

Теперь предположим, что мы используем для(Т) верхнюю квадратичную границу, т.е.

(2.1.166)

К)<

График для g(Y) и верхняя граница показаны на рис. 2.1,11. Из графиков следует, что

E[g{Y)\<E

Так KaKiig(7)] является вероятностью хвоста, как это следует из (2.1.165), мы получили границу Чебышева.

Верхняя граница

(Г/8)

-5 О

Рис. 2.1.11 Квадратичная верхняя граница для g(Yy используемая для получения вероятности хвостов (фаница Чебышева)

Для многих практических приложений эта чебышевская граница чрезмерно груба. Это можно объяснить неточностью квадратичной функции как верхней границы g(Y). Имеется много других функций, которые можно использовать в качестве верхней границы g(Y). В частности, граница Чернова часто оказывается более плотной.

Граница Чернова. Чебышевская граница, данная выше, включает площадь, ограниченную обоими хвостами ФПВ. В некоторых приложениях мы интересуемся лишь площадью, офаниченной одним хвостом: либо в интервале (5,оо), либо в интервале (-оо,-5). В таком случае мы можем получить весьма плотную верхнюю границу путем огибания функции g(Yj посредством экспоненты с параметром, который может оптимизировать верхнюю границу так плотно, насколько это возможно. Конкретно мы рассмотрим вероятность хвоста в интервале (5,со). Введем огибающую для g(Y) из соотношения

g(Y)<e\ (2.1.167)

где g(Y) теперь определена как

, , fl (7>5),

а V > О - параметр, который следует оптимизировать.

Графики для g(Y) и экспоненциальной верхней границы даны на рис. 2.1.12. Математическое ожидание g(Y) равно

мг.&)

(2.1.169)

E[giY)\PiY>d)<E Эта граница справедлива для любых v>0.

Наиболее плотную верхнюю границу можно получить путем выбора значений.

которые минимизируют Е

Необходимое условие минимизации

= 0.

(2.1.170)