откликается тремя битами, по числу функциональных генераторов (и = 3). Пронумеруем функциональные генераторы и их выходы в соответствии с порядком считывания мультиплексором (1, 2 и 3). Затем, поскольку с первым функциональным генератором соединена только первая ячейка (сумматор по modi не нужен) генератор можно отобразить вектором

g,=[lOO].

Второй функциональный генератор соединен с ячейками 1 и 3. Следовательно,

g3=[l0l].

Наконец,

g3=[Hl].

Генераторы (порождающие полиномы) для этого кода обычно дают в восьмеричной форме как g=(4, 5, 7). Мы заключаем, что, когда к - \, требуются и генераторов, каждый размерностью К, чтобы описать кодер.

В общем случае при к> \ а кодовом ограничении К эти п генераторов отображаются Кк -мерными векторами, как оговорено выше. Следующий пример иллюстрирует случай, когда к = 2 и о = 3.

Пример 8.2.1. Рассмотрим свёрточный кодер со скоростью кода 2/3, показанный на рис. 8.2.3. В этом кодере каждый раз два бита поступают на вход регистров сдвига, а на выходе генерируется три бита.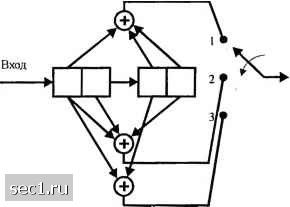

Выход

Рис. 8.2.3. Свёрточный кодер с К=2, к=2, и=3

Генераторы определяются векторами g,-[l01l], g,=[llOl], g3=[l010]. В восьмеричной форме g-(13, 15, 12)

Имеются три альтернативных метода, которые часто используются для описания свёрточного кода. Это древовидная диаграмма, решётгчатая диаграмма и диаграмма состояний. Для примера, древовидная диаграмма для свёрточного кодера, показанного на рис. 8.2.2, иллюстрируется на рис. 8.2.4.

Предположим, что кодер находится первоначально в нулевом состоянии (во всех ячейках нули). Диаграмма показывает, что, если первый вход О - выходная последовательность ООО, а если первый вход 1 - выходная последовательность 111. Теперь, если первый вход 1, а второй О - второй набор выходных битов 001. Продвигаясь по дереву видим, что если третий входной бит О, тогда выходной 011, если же третий выходной бит 1, то выход 100. Видим, что частная последовательность обуславливает выбор узла дерева, а правило движения по ветвям дерева такое - надо двигаться к верхней

ветви, если следующий бит О и к нижней, если следующий бит 1. Таким образом, траектория частного пути по дереву определяется входной последовательностью.

00(1

(.11

Piic. S.2.4. Древовидная днаф;шма для сверточного кода, имеющего скорость 1/3, А:--3

Внимательное наблюдение за деревом, показанном на рис. 8.2.4, обнаруживает, что структура повторяет себя после третьего такта. Правый столбец выходных «троек» бит распадается на две одинаковые совокупности по 8 «троек». Это поведение согласуется с тем фактом, что кодовое ограничение К = 3. Это значит, трёхбитовые выходные последовательности на каждом такте определяются входным битом и двумя предыдущими входными битами, т.е. двумя битами, содержащимися в первых двух ячейках регистра сдвига. Бит в последней ячейке регистра сдвига перемещается направо (покидает регистр) ii не влияет больще на выход. Так что мы южeм сказать, что трёхбитовая последовательность выхода для каждого входного бита определяется входным битом и четырьмя возможными состояниями регистра сдвига, обозначенными «~00, Ь=0\, с-10, (h\l. Если пометить узлы дерева этими же метками, найдем, что на третьем такте имеются дна узла с пометкой с/, два с пометкой h, два с пометкой с и два с пометкой d Теперь видим, что все ветви, исходящие из двух узлов с одинаковой меткой (одинаковым состоянием) являются идентичными в том смысле, что они генерируют одинаковые выходные последовательности. Это означает, что два узла, имеющие одинаковую метку, можно слить. Если мы это сделаем в дереве, показанном на рис. 8.2.4 , мы получим другую диаграмму, которая более компактна, именно получим решётку. Для примера решётчатая диаграмма для сверточного кодера рис. 8.2 2 показана на рис. 8.2.5.

Чтобы изучить эту диаграмму, договоримся о том, что сплошные линии означают выходы, генеририруемые входом О, а пунктирные - выходы, генеририруемые входом 1. В примере, которьиТ мы рассматриваем, видим, что после начального состояния решётка содержит четыре узла на каждом шаге, соответствующие четырем состояниям регистра сдвига а, Ь, с и d. После второго шага каждый узел в решётке имеет два входных пути и два выходных. Из выходных путей один соответствует входу О, а второй - входу 1.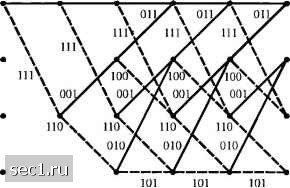

Уота110вившнйС1 режим

Рис. 8.2.5. Решётчатая диаграмма д-пя свёрточного кода, имеющего скорость 1/3 Л.3

Поскольку выход кодера определяется входом и состоянием кодера, ещё более компактной, чем решётка, является диаграмма состояний. Диаграмма состояний - это просто граф возможных состояний кодера и возможных переходов из одного состояния в другое. Для примера на рис. 8.2.6 показана диаграмма состояний для кодера, показанного на рис. 8.2.2.

Сосюшше Ь 01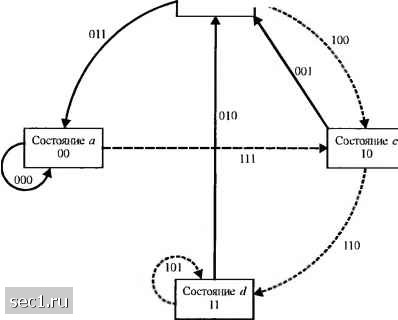

Рис. 8.2.6. Диаграмма состояний для свёрточного кода, имеющего скорость 1/3, К=3

Эта диаграмма показывает, что возможные переходы таковы

-с,с-

-b,c->d ,d->b,d->d,

где a->3 означает переход из состояния а в Р, когда входной бит 1. Три бита,

показанных далее на каждой ветви диаграммы состояний, представляют выходные биты. Пунктирная линия на графе означает, что входной бит 1, в то время как сплошная линия указывает, что входной бит 0.