Пример 8.2.2. Рассмотрим свёрточный код со скоростью 2/3, Л=2, описанный в примере 8.2.1 и показанный на рис. 8.2.3. Первые два входных бита могут быть 00, 01, 10 или 11. Соответствующие выходные биты-ООО, 010, 111, 101. Когда следующая пара входных битов входит в кодер, первая пара передвигается в следующую ячейку. Соответствующие выходные биты зависят от пары битов, переместившихся во вторую ячейку и новой пары входных битов. Следовательно, древовидная диаграмма для этого кода, показанная на рис. 8.2.7, имеет четыре ветви на узел, соответствующие четырём возможным парам входных символов. Поскольку кодовое ограничение кодера = 2, дерево начинает повторяться после второго шага. Как показано на рис. 8 2 7, все ветви, исходящие из узла, обозначенного а (состояния а) дают идентичные выходы. Путём слияния узлов, имеющих одинаковое название, мы получаем решётку, показанную на рис. 8.2.8. Итоговая диаграмма состояний для этого кодера показана на рис. 8.2.9.

Рис. 8.2.7. Древовидная диаграмма для сверточного кода, имеющего параметры К-1, к=2, п-л

Для обобщения отметим, что свёрточный код со скоростью к/п и кодовым ограничением А!" характеризуется 2*" ветвями, уходящими от каждого узла на древовидной диаграмме. Решётка и диаграмма состояний имеют (каждая из них) 2*" возможных состояний. Имеются 2* ветвей, входящих в каждое состояние, и 2* ветвей, покидающих каждое состояние (для решётки и дерева это верно после наступления установившегося режима)

ООО а ООО а ООО а ООО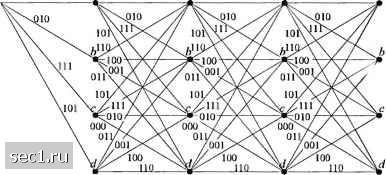

Рис. 8.2.8. Решётчетая диафамма дтя сверточного кода, имеющего параметры К1, kl. п=3

Три типа диаграмм, описанных выше, используются также для представления недвоичных свёрточных кодов. Если число символов в алфавите равно q 2*, к>\, результирующий недвоичный код можно также представить как эквивалентный двоичный код. Следующий пример рассматривает свёрточный код этого типа.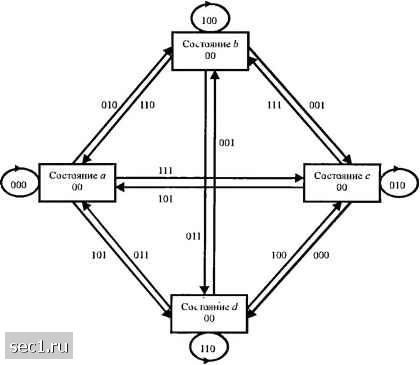

Рис. 8.2.9. Диафамма состояний для свёрточного

кода, имеющего параметры А. 2, к-1, п 2

Пример 8.2.3. Рассмотрим свёрточнь й код, генерируемый кодером, показанном на рис. 8.2.10 Этот код можно описать как двоичный свёрточный код с параметрами К -2, к = 2, А/ - 4, Rc = 1/2 и с генераторами

g,=[l010], g3=[010l], g3=[lll0], g,=[l00l].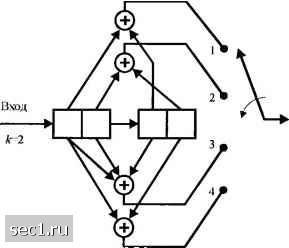

Выход

Рис. 8.2.10. Свёрточный кодер с К-2, кг2, п=3

За исключением различия в скорости, этот код похож по форме на свёрточный код со скоростью 2/3, к=2, рассмотренный в примере 8.2.1.

Альтернативно, код, генерируемый кодером рис. 8.2.10, можно описать как не двоичный (/=4) код с одним четырехпозпционным символом на входе и двумя четырехпозиционных символов на выходе. Действительно, если выходные символы кодера трактуются модулятором и демодулятором как б/-ичные (4), которые передаются по каналу посредством некоторой М-ичный (М=4) модуляции, код можно соответственно рассмотреть как недвоичный.

В любом случае, древовидные, решётчатые диафаммы и диаграммы состояний независимы от того, как мы смотрим на код. Это значит, что этот частный код, характеризуется деревом с четырьмя ветвями, исходящими от каждого узла, или решёткой с четырьмя возможными состояниями и четырьмя ветвями, входящими и покидающими каждое состояние, или, что эквивалентно, посредством диаграммы состояний, имеющей те же параметры, что и решётка.

8.2.1. Передаточная функция сверточного кода

Дистанционные свойства и характеристики качества (вероятность ошибки) сверточного кода можно получить из его диаграммы состояний. Поскольку свёрточный код линейный, набор расстояний Хемминга мех<ду кодовыми последовательностями-, генерируемыми на определённом шаге дерева и последовательностью из одних нулей, такой же, как набор расстояний кодовых последовательностей по отношению к другой кодовой последовательности. Следовательно, мы предположим, без потери общности, что входом кодера являегся последовательность из одних нулей.

Диаграмма состояний, показанная на рис. 8.2.6, будет использована для демонстрации метода получения дистанционных свойств сверточного кода. Сначала мы пометим ветви на диаграмме состояний как £) = 1, £), D или , где показатель у D означает расстояние Хемминга меаду выходной битовой последовательностью, соответствующей ветви, и выходной последовательностью, соответствующей ветви из одних нулей. Собственную петлю у узла а можно исключить, поскольку она ничего не вносит в дистанционные свойства кодовой последовательности относительно кодовой последовательности из одних нулей. Дальше, узел а расщепляется на два узла, один из них представляет вход, а другой выход диаграммы состояний. Рис. 8.2.11 иллюстрирует результирующую диаграмму.

Рис. 8.2.11. Диаграмма состояний для сверточного кода, имеющего скорость 1/3, К=2

Мы используем эту диаграмму, которая теперь состоит из пяти узлов, поскольку узел а был расщеплен на два узла, для написания четырех уравнений состояния: