X-DX + DX,, X,-DX + DX„ X, = D-X + DX„ X = DX,.

Передаточная функция кода определяется как T{D) = XjX состояния, данные выше, мы получим

(8.2.1) Решив уравнения

T{D) =-7 = + 2D + 4£)° + 8D4... = 2 aD

1-2D

(8.2.2)

(8.2.3)

где, по определению,

(четные J) [ О (нечетные d).

Передаточная функция этого кода указывает на то, что имеется единственный путь с расстоянием Хемминга d=6 от пути из одних нулей, который сливается с путём из одних нулей при данном узле. Из диаграммы состояний, показанной на рис. 8.2.6, или решётчатой диаграммы, показанной на рис. 8.2.5, видно, что путь с d=6 это асЬе. Нет других путей из узла а до узла е, имеющих расстояние d=6. Второе слагаемое в (8 2 2) указывает на то, что есть два пути от узла а до узла е, имеющих расстояние d=S. Снова из диаграммы состояний или решётки мы видим, что этими путями являются acdbe и acbcbe. Третье слагаемое в (8.1.2) указывает, что есть четыре пути с расстоянием d-\0 и так далее. Таким образом, передаточная функция даёт нам дистанционные свойства свёрточного кода. Минимальное расстояние кода называется лшнимальным свободным расстоянием и обозначается d. В нашем примере d = 6.

Передаточную функцию можно использовать для получения более детальной информации, чем только расстояния различных путей. Введём множитель Л для всех переходов ветвей, вызванных входным битом 1. Тогда, поскольку каждая ветвь пересекается, совокупный показатель Л увеличивается на единицу только тогда, когда переход ветви обусловлен входным битом 1. Далее мы вводим множитель J для каждой ветви диаграммы состояний так, что показатель ./ будет служить счётной величиной, указывающей число ветвей для любого данного пути от узла а к узлу е. Для свёрточного кода со скоростью 1/3 в нашем примере диаграмма состояний, которая объединяет суммируемые множители J aN, показана на рис. 8.2.12.

»--

------

JNI>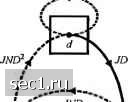

Рис. 8.2.12. Диаграмма состояний для cвёpтoшoгo кода, имеющего скорость Ш, К=3

Уравнения для диаграммы состояний, показанной на рис. 8.2.12, таковы:

X, = JDX + .JDX„

X = JMDX + JNDX, X, = JNDX + JND~X„ X = JDX.

(8.2.4)

Решая эти уравнения, получаем передаточную функцию

Эта форма передаточной функции даёт свойства всех путей сверточного кода. Это значит, что первое слагаемое в выражении T{D,N,J) указывает на то, что путь с расстоянием d = 6 имеет длину 3 и что из трёх информационных битов один «1». Второе и третье слагаемые в выражении T{D,N,J) указывают на то, что из двух слагаемых с расстоянием d = S одно длиной 4, а второе длиной 5. Два из четырёх информационных бит в пути длиной 4 и два из пяти информационных бит в пути длиной 5 являются «1».

Таким образом, показатель множителя J указывает длину пути, который сливается первый раз с путём из одних нулей, показатель множителя N указывает число «1» в информационной последовательности для этого пути, а показатель D указывает расстояние от последовательности кодированных битов этого пути от последовательности с одними нулями.

Множитель./ особенно важен, если мы передаем последовательность конечной длины, скажем, т битов. В этом случае свёрточный код повторяется после т узлов или т ветвей. Это подразумевает, что передаточная функция для усечённого кода получается при

усечении T{D,N,J) по слагаемому ./". С другой стороны, если мы передаем экстремально длинную последовательность, т.е. существенно неограниченную по длине последовательность, мы хотим подавить зависимость T(D,N,J) от параметра J. Это легко выполнить, положив J=l. Так для примера, данного выше, мы имеем

T(D. N.l) = T(D. /V) = = ND + IN-D + AND° +.. .= V aN-O". (8.2.6)

где коэффициенты {а} определены (8.2.3).

Процедуру, которую мы описали в общих чертах выше для определения передаточной функции двоичного сверточного кода, легко расширить на недвоичные коды. В следующем примере мы определим передаточную функцию для недвоичного сверточного кода, ранее введённого в примере 8.2.3.

Пример 8.2.4. Свёрточный код, показанный на рис. 8.2.10, имеет параметры К-2, к = 2, п = 4.

Допустим, что мы трактуем код как недвоичный. Так, вход кодера и выход кодера можно трактовать как четверичные символы. В частности, если мы трактуем вход и выход как четверичные символы 00, 01, 10 и 11, то расстояние, измеряемое в символах между последовательностями 0111 и 0000, равно 2. Далее предположим, что входной символ 00 декодируется как символ И, тогда мы имеем одну ошибку в символе. Это соглашение, применённое к свёрточному коду, показанному на рис. 8.2.10, приводит к диаграмме состояний, иллюстрируемой рис. 8.2.13.

Из неё мы получаем уравнения состояний:

X, = NJD-X + NJDXb + NJDX + NJDXj,

X = NJDX + NJDX + NJDX + NJDX,, X = NJD-X, + NJDX + NJDX + NJDX,, X, = JDix,+.X, + X,).

Состояние b 01

Состояние a 00

00-0 01 = 1 10-2 11=3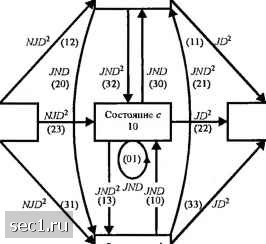

Состояние e 00

Состояние d 11

Рис. 8.2.13. Диафамма состояний для недвоичного свёрточного кода, имеющего параметры К=2, к=2, скорость 1/2

Решение этих уравнений приводит к передаточной функции

TiD,N,j) =

(8.2.8)

1-2JD-NJD

Это выражение для передаточной функции особенно применимо тогда, когда четверичные символы на выходе кодера отображаются в соответствующий ансамбль четверичных сигналов л;/), «/ = 1,2,3,4, например, четырьмя ортогональными сигналами. Таким образом здесь имеется взаимно-однозначное соответствие между кодовыми символами и сигналами.

Альтернативно, для примера, выход кодера можно передать как последовательность двоичных символов посредством двоичной ФМ. В таком случае следует измерять расстояние в битах. Если использовать такое соглашение, диаграмма состояний имеет вид рис. 8.2.14.

Решение уравнений состояний, полученное из этой диаграммы состояний, приводит к передаточной функции, которая отличается от той, которая дана (8.2.8).

Некоторое свёрточные коды проявляют характерное поведение, называемое катастрофическим размиоэюением ошибок.

Когда код, который имеет такие характеристики, используется в двоичном симметричном канале, возможно, при ограниченном числе ошибок в канале, неограниченное число ошибок декодирования. Такой код можно идентифицировать из его диаграммы состояний. Она может содержать путь с нулевым расстоянием (путь с множителем D° = l) от некоторого ненулевого состояния обратно в то же самое состояние. Это означает, что может образоваться петля вокруг этого пути с нулевым расстоянием неограниченное число раз без увеличения расстояния относительно пути с одними нулями. Но если эта собственная петля соответствует передаче 1, декодер будет