Если к >\, эквивалентная вероятность ошибки на бит получается путём деления (8.2 26) и (8.2.27) на к .

Выражения для вероятности ошибки, данные выше, базируются на предположении, что кодовые символы передаются двоичной ФМ при когерентном приеме. Результаты для Ph также верны для четырёхфазной когерентной ФМ, поскольку эта техника модуляции/демодуляции эквивалентна двум независимым (квадратурным по фазе) двоичным системам ФМ. Для другой техники модуляции и демодуляции, такая как когерентная и некогерентная ЧМ, результаты можно приспособить путём пересчета парной вероятности ошибки P{d). Это значит, что выбор техники модуляции и демодуляции, использованной для передачи кодированной информационной последовательности, влияет только на расчет P-Xd). Расчёт остаётся тем же.

Хотя приведенные выше расчёты вероятности ошибки при декодировании по Витерби сверточного кода применимы для двоичных свёрточных кодов, относительно легко обобщить их на недвоичные свёрточные коды, в котором каждый недвоичный символ отобрамается различным сигналом. В частности, коэффициенты (Р} в выражении

производной T{D,N), даваемые (8.2.25), представляют число ошибок в символах в двух путях, разделенных расстоянием(числом символов) в d символов. Снова мы обозначим вероятность ошибки при парном сравнении двух путей, которые разделены расстоянием d, через Pid). Тогда вероятность ошибки символа, для Аг-битового символа, ограничена сверху

Вероятность ошибки символа можно превратить в эквивалентную вероятность ошибки на бит. Для примера, если используются 2*" ортогональных сигналов для передачи А--битовых символов, эквивалентная вероятность ошибки на бит равна /д, умноженной

на множитель 2* /(2* - l), как указано в главе 5.

8.2.4. Вероятность ошибки при декодировании жёстких решений

Теперь рассмотрим качество, достижимое алгоритмом декодирования Витерби в двоичном симметричном канале. При декодировании жёстких решений сверточного кода метрики для алгоритма Витерби являются расстояния Хемминга между принимаемой

последовательностью и 2 выжившими последовательностями в каждом узле решётки. Как при нашей трактовки декодирования мягких решений, мы начнем с расчета вероятности первого ошибочного события. Считается, что передается путь из одних нулей. Предположим, что путь, который сравнивается с путём из одних нулей в некотором узле В, имеет расстояние d относительно пути из одних нулей. Если d нечётно, путь из одних нулей будет выбран без ошибок, если число ошибок в принимаемой последовательности меньше, чем (с/ +1); в противном случае будет выбран неправильный путь. Следовательно, вероятность выбора неправильного пути равна

РМ= t [УО-рГ> (8-2.28)

где р вероятность ошибочного приема символа в двоич1ом симметричном канале. Если d четно, то неправильный путь выбирается, когда число ошибок превышает -kd. Если число ошибок равно 2d, то имеется связь между метриками двух путей, которую можно

27* . " 419

разрешить случайным выбором одного из путей; так что ошибка возникнет в половине случаев. Следовательно, вероятность выбора неправильного пути равна

a X 1

(8.2.29)

Как указано в разделе (8.2.3), имеется много возможных путей с различными расстояниями, которые сливаются в данном узле с путем из одних нулей. Следовательно, вероятность первого ошибочного события не являются точным выражением. Однако мы можем определить верхнюю границу посредством суммирования парных ошибок Picf) по всем возможным путям, которые сливаются при данном узле с путём из одних нулей. Таким образом мы получим объединенную границу

(8.2.30)

где коэффициенты {а,} представляют число путей, соответствующих набору расстояний [j] . Эти коэффициенты являются коэффициентами в выражении передаточной функции У(Л)или T{D,N).

Вместо использования выражения для PjjJ), даваемое (8.2.29) и (8.2.30), мы можем использовать верхнюю границу

pM<Up[\-p)

(8.2.31)

которая была дана в разделе 8.1.5. Использование этой границы в (8.2.30) дает свободную верхнюю границу для вероятности первого ошибочного события в виде

K<lLciUp{\-p)\ <r{D)

d=d„

(8.2.32)

Теперь определим вероятность ошибки на бит. Как в случае декодирования мягких решений, мы используем тот факт, что показатели в множителях N, которые имеются в

передаточной функции T{D,N) указывают на число ненулевых информационных символов, которые ошибочно приняты, когда неправильный путь выбран вместо пути из одних нулей. Путём дифференцирования P{D,N) по N и приравнивания N=\ в результате получим значения для соответствующих вероятностей первых ошибочных событий P,(i/). Так мы получим выражение для верхней границы вероятности ошибки на бит в виде

Pb<lldP2id),

(8.2.33)

где iPj}- коэффициенты в выражении для производной T{D,N), рассчитанной при N = I. Для (с/) мы можем использовать или выражения, данные (8.2.28) и (8.2.29), или верхнюю границу (8.2.31). Если используется последняя, верхнюю границу для Р можно выразить так

сГГ{Р, N)

Ы=1 D=4p(. р)

(8.2.34)

Если А > 1, результат (8.2.33) и (8.2.34) для надо разделить на к . На рис. 8.2.15 дано сравнение вероятности ошибки для свёрточного кода со скоростью 1/3, К-Ъ при декодировании мягких и жёстких решений. Заметим, что верхняя граница

Чернова (8.2.24) хуже на 1 дБ относительно плотной верхней границы (8.2.33) в соединении с (8.2.28) и (8.2.29). Преимущество границы Чернова - простота вычисление. Сравнивая качество декодирования мягких и жёстких решений, отметим, что разница, получаемая от верхних границ примерно 2, 5 дБ для 10"* < Р, < 10".

В заключение мы хотим напомнить, что средняя по ансамблю вероятность ошибки для сверточного кода в дискретном канале без памяти, так же как в случае блокового кода, можно выразить через предельную скорость 7 (доказательство см. Витерби и Омура,

1979)

-j-iV;

где q - число входных символов канала. К - кодовое ограничение, R - скорость кода, У,-предельная скорость, определённая в разделе 7.2 и 8.1. Заключения, полученные путём вычисления R для различных условий в канале, применимы как к блоковым, так и

свёрточным кодам.

10"

2 -

5 -

10-«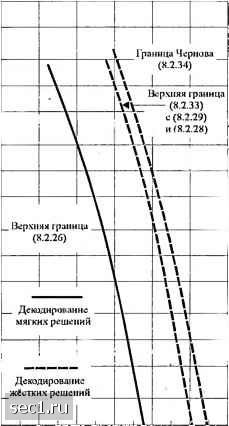

4 б 8 10

ОСШ на бит, Yv ЛБ

Рис. 8.2.15. Сравнение декодирошшия мягки.ч и жёстки.х решений для сверточного кода с К=3. к=1, «-3

8.2.5. Дистанционные характеристики двоичных свёрточных кодов

В этом подразделе мы хотим свести в таблицу минимальные свободные расстояния и генераторы для нескольких свёрточных кодов с малыми кодовыми ограничениями и для