итоге каждьи"! символ внешнего кода отображается в одно из 32 кодовых слов кода Адамара.

Вероятность ошибочного декодирования символа внутренним кодом можно определить из результатов качества блоковых кодов, данных в разделах 8.1.4 и 8.1.5, соответственно, для декодирования мягких и жёстких решений.

Сначала предположим, что во внутреннем декодере осуществляется жёсткое решение с вероятностью ошибки декодирования кодовых слов (символов внешнего кода), обозначенную /3,, так как Л/= 32 .Тогда качество внешнего кода и, следовательно, качество каскадного кода можно получить, используя эту вероятность ошибки в соед1шении с передаточной функцией для 5-дуального кода, определенной в (8.2.32).

С другой стороны, если декодирование мягких решений используется во внешнем и внутреннем декодерах, метрики для мягкого решения о каждом принимаемом кодовом слове кода Адамара передаются на алгоритм Витерби, который вычисляет результирующие метрики для конкурирующих путей решётки. Мы дадим численные результаты качества каскадных кодов этого типа в нашей дискуссии о кодировании в каналах с релеевскими замираниями.

8.2.7. Другие алгоритмы декодирования свёрточных кодов

Алгоритм Витерби, описанный в разделе 8.2.2, это оптимальный алгоритм декодирования для свёрточных кодов. Однако он требует вычисления 2* метрик каждого

узла решётки и хранения 2*""" метрик и 2* " выживших последовательностей, каждая из них имеет длину около SkK бит Вычислительное время и память для хранения, требуемого для реализации алгоритма Витерби, делают его практически неприемлемым для свёрточных кодов с большим кодовым ограничением.

Еще до открытия оптимального алгоритма Витерби, были придуманы другие алгоритмы для декодирования свёрточных кодов. Самым ранним был алгоритм последовательного декодирования, впервые предложенный Возенкрафтом и впоследствии модифицированный Фано (1963).

Последовательный алгоритм декодирования Фано ищет наиболее правдоподобный путь по дереву или решётке путём проверки каждьиТ раз одного пути. Приращение, добавляемое к метрике вдоль ветви пропорционально вероятности принимаемого сигнала для этой ветви, как в алгоритме Витерби, за исключением того, что к метрике каждой ветви добавляется отрицательная константа прибавляется. Величина этой константы выбирается так, что метрика правильного пути будет в среднем увеличиваться, в то время как метрика для любого неправильного пути в среднем будет уменьшаться. Путём сравнения метрики претендующего пути с меняющимся (увеличивающимся) порогом алгоритм Фано обнаруживает и отвергает неправильные пути.

Для большей конкретности рассмотрим канал без памяти.

Метрика для /-го пути по дереву или решётке от первой ветви до В-\\ ветви можно выразить так

СЛ)=1:2:<. (8.2.42)

j-i т-\

i!:=QS. 7 V (8.2.43)

в (8.2.43) выходная последовательность демодулятора, pirJcjl) означает условную ФПВ /j„, при условии кодового бита cj, (т-й бит в j-й ветви /-го пути), а. Ж-

положительная константа. Л выбирается, как сказано выше, так, что неправильные пути будут иметь уменьшающиеся метрики, в то время как правильный путь в среднем увеличивает метрику. Заметим, что член р{г„) в знаменателе не зависит от кодовой

последовательности и, следовательно, мох<ет быть включен в постоянную.

Метрика, определённая (8.2.43), в общем применима при декодировании как жёстких, так и мягких решений. Однако она может быть особенно упрощена, когда используется декодирование жёстких решений. В частном случае, если мы имеем ДСК с переходной вероятностью ошибки р, метрика для каждого принятого символа, согласующаяся с формулой (8.2.43), определяется так

\og\2(\ р] log. 1р-К

при при

(8.2.44)

г,„,- выходы жёстких решении демодулятора,

cjj- W-й кодовый символ в j-й ветви /-го пути дерева.

- скорость кода.

Заметим, что эти метрики требуют хотя бы приближённого знания вероятности ошибки

Пример 8.2.6. Предположим, что для передачи информации по ДСК с вероятностью ошибки р = 0,1 используется двоичный свёрточный код со скоростью R - l/З. Вычисление согласно (8.2.44) дает

0.52 Тбё

-2.65

JIII Ill

Для упрощения расчётов метрики (8.2.45) можно нормировать, аппроксимируются так:

(8.2.45)

Они хорошо

1 г=с

jm jп

(8.2.46)

Поскольку скорость кода равна 1/3, то кодер имеет три выходных символа на каждый входной символ. Тогда метрики ветвей, согласующиеся с (8.2.46), равны

или, что эквивалентно,

H;-l-2t/, (8.2.47)

где d - хеммингово расстояние трёх принятых бит от трёх битов на ветви.

Таким образом, метрики р. просто связаны с расстоянием Хемминга между

принимаемыми символами и кодовыми символами /-й ветви /-го пути.

Первоначально декодер можно заставить выбирать правильную траекторию путём передачи известной цепочки данных. Тогда он продвигается вперед от узла к узлу, выбирая наиболее вероятную (с большей метрикой) ветвь в каждом узле и увеличивая порог так, что его изменение никогда не больше, чем некоторая заранее выбранная величина, скажем, I. Теперь предположим, что аддитивный шум (при декодировании мягких решений) или ошибки демодуляции, возникающие из-за шума в канале (при декодировании жёстких

решений) заставят декодер принять неверный путь, поскольку он кажется более правдоподобным, чем правильный путь. Эта иллюстрирует рис. 8.2.17.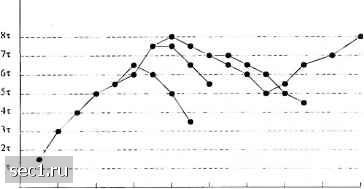

2 4 б S 10 12

IIoMti LiiMiioJl;i

Рис. 8 2.17. Пример поиска пути при послсдовательно.м декодировании [Jordan (1966). © 1966 /ЛЩ

Поскольку метрики неверного пути в среднем уменьшаются, метрика упадет ниже текущего порога, скажем т„. Если это случится, декодер возвращается обратно и берёт альтернативный путь по дереву (решётке) с меньшей метрикой ветви, в попытке найти другой путь с большей метрикой, которая превосходит порог т,. Если приходит удача в альтернативном пути, это продолжается вдоль пути все время, и выбирается наиболее правдоподобная ветвь в каждом узле. С другой стороны, если не существует пути, который превышает порог т„, порог уменьшается на величину т и декодер возвращается к первоначальному пути. Если первоначальный путь не находится выше нового порога, декодер начинает обратный поиск других путей. Эта процедура повторяется с уменьшением порога на т при каждом повторении до тех пор, пока декодер не наПдет путь, который остаётся выше установленного порога. Упрощённая структурная схема алгоритма Фано показана на рис. 8.2.18.

Алгоритм последовательного декодирования требует буферную память в декодере для хранения поступающих данных декодирования в течение периодов, когда декодер ищет альтернативные пути. Когда поиск заканчивается, декодер должен быть в состоянии обрабатывать демодулированные символы достаточно быстро, чтобы освободить буфер для начала нового поиска. Иногда в течение экстремально длинных поисков буфер может переполниться. Это вызывает потерю данных, которые можно восстановить повторением потерянной информации. В этой связи мы хотим напомнить, что предельная скорость 7, имеет особый смысл при последовательном декодировании. Это скорость, выше которой среднее число операций декодирования на декодированный символ становится неограниченным и оно выражает предельную вычисттельпую скорость 7„„. На практике последовательные декодеры обычно работают при скоростях, близких к 7,.

Алгоритм последовательного декодирования Фано успешно применяется в различных системахсвязи. Его качество по вероятности ошибки сравнимо с декодером Витерби. Однако по сравнению с декодером Витерби последовательное декодирование имеет значительно большую задержку декодирования. С другой стороны, последовательное декодирование требует меньше памяти, чем декодирование по Витерби, и, следовательно, оно является привлекательным для свёрточных кодов с большим кодовым ограничением.