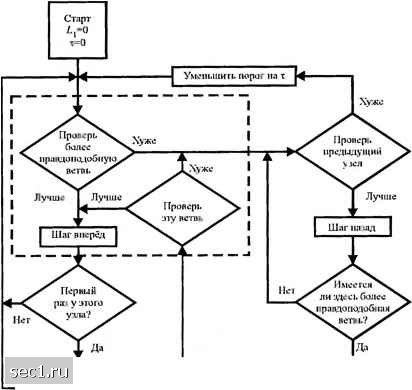I У1к-личить порог на t I I-

Рис. 8.2.18. Упрощённа структлра алгоритма Фано [Jonhii (19Г)б), © 19Г)Г) IEEE]

Исследования вычислительной сложности и требований к памяти для последовательного декодирования вызывают интерес, и они все еще продолжаются. Для анализа этих вопросов и других характеристик алгоритмов Фано интересующемуся читателю рекомендуются книги Галлагера (1986), Возенкрафта и Джекобса (1965), Сэвейдж (1966) и Форни (1974). Другой тип алгоритма последовательного декодирования, названный стек-алгоритмом, был предложен независимо Зигангировым (1966) и

Елинеком (1969). В противовес алгоритму Витерби, который сохраняет траектории 2"" * путей и соответствующих метрик, стек-алгоритм последовательного декодирования работает с несколькими путями и их соответствующими метриками. В стек-алгоритме более вероятные пути упорядочиваются согласно их метрик, причём в верхней части (в голове стека) располагается путь, имеющий наибольшую метрику. На каждом шаге алгоритма только путь в голове стека проверяется по разветвлению. Это приносит 2* продолжений и их соответствующих метрик. Эти 2* продолжения вместе с другими путями затем упорядочиваются согласно величинам их метрик, и все пути с метриками, которые располагаются ниже некоторой выбранной величины от метрики главного пути, отбрасываются. Затем процесс продолжения путей с наибольшими метриками повторяется. Рис. 8.2.19 иллюстрирует несколько первых шагов стек-алгоритма.

Очевидно, что если ни одно из 2*" продолжений пути с наибольшей метрикой не остаётся в голове стека, следующий шаг поиска выполняет продолжение другого пути, который приближается к голове стека. Отсюда следует, что алгоритм не всегда даёт быстрое продвижение по начатой траектории при любой итерации. Следовательно, некоторую величину памяти нужно зарезервировать для вновь принятых символов и ранее принятых символов для того, чтобы позволить алгоритму расширить поиск по одному из более коротких путей, когда такой путь достигает головы стека.

с1 001

Принятая последовательность:

b 010

Скорость код.т I 3 Метрика пени \-2cl ,1- расстояние Хемминга

110 Oil

Стек с накопленными метриками путей

Рис. 8.2.19. Пример работы стек алгоритма для декодирования свёрточного код;, со скоростью 1/3

Из сравнении стек-алгоритма с алгоритмом Витерби следует, что стек-алгоритм требует малого числа сравнений метрик, но его вычислительная экономия в большой степени снижается за счёт вычислений, требуемых для упорядочивания стека после каждой итерации. По сравнению с алгоритмом Фано, стек-алгоритм в вычислительном отношении проще, поскольку здесь нет возвращения по тому же пути, как это делает алгоритм Фано. С другой стороны, стек-алгоритм требует больше памяти, чем алгоритм Фано.

Третья альтернатива оптимального декодера Витерби-это метод, названный декодированием с обратной связью (Хеллер 1975), который был разработан для декодирования в ДСК (декодирование жёстких решений). При декодировании с обратной связью декодер делает жёсткое решение об информационном символе на 7-м шаге, основываясь на метриках, вычисленных от7-го до (/+m)-ro шага, где т - выбранное целое число. Таким образом, решение об информационном символе в пользу О или 1 зависит от того, каково минимальное расстояние по Хеммингу для пути, который начинается на /-м шаге и кончается на {]+т)-м шаге и сколько содержится «О» или «1» в ветви, исходящих от шага j. Решение выносится один раз об информационном символе на j шаге, и только часть дерева, которая связана с этим символом, сохраняется (половина путей, исходящих из узла 7"), а остальные пути исключаются. Так осуществляется обратная связь в декодере. Следующий шаг заключается в расширении части дерева, которая вышла до шагау+И-я? и

рассмотрении путей от шага (/+1)-го до (/+1+т)-го для принятия решения о символе на шаге 7+1. Так процедура повторяется на каждом шаге. Параметр ш-это просто число шагов по дереву, которое декодер учитывает при вынесении жёсткого решения. Поскольку большая величина т ведет к большой величине памяти, желательно т выбрать как можно меньше. С другой стороны, т должно быть достаточно большим, чтобы избежать существенного ухудшения качества. Чтобы сбалансировать эти два противоречивых требования, т обычно выбирается в области К <т <2К, где АГ-кодовое ограничение. Заметим, что эта задержка при декодировании значительно меньше, чем задержка при использовании алгоритма Витерби, которая обычно около 5К.

Пример 8.2.7. Рассмотрим использование декодера с обратной связью для сверточного кода со скоростью 1/3, показанного на рис. 8.2.2. Рис. 8.2.20 иллюстрирует древовидную диаграмму и операции декодера с обратной связью при w=2. Это значит, что при декодировании символа ветви j, декодер рассматривает пути на ветвях и J+2. Начиная с первой ветви, декодер рассчитывает восемь метрик (расстояние Хемминга) и решает, что символ в первой ветви является О, если путь с минимальным расстоянием находится в верхней части дерева и, что символ 1, если путь с минимальным расстоянием находится в нижней части дерева. В этом примере принимаемая последовательность для первых трёх ветвей полагается такой 101 111 110, поэтому путь с минимальным расстоянием находится в верхней части дерева, следовательно, первый выход символа декодера 0.

Следующие шаги сводятся к расширению верхней части дерева (той части дерева, которая выжила) на одну ветвь и к вычислению восьми метрик в ветвях 2, 3 и 4. Для предположения входной последовательности 111 110 011 путь с минимальным расстоянием находится в нижней части секции дерева, вычислившей после первого шага. Итак, второй выходной символ декодера 1. Третий шаг заключается в расширении этой нижней част;! дерева и повторении процедуры, описанной для двух первых шагов.

.,.000

"иг. тггг

Д11:.

I. lio

Принятая Шаг

nocjK-дова- 1 , , , . .. тельность: 101 JIXl

Ш.1Г I: М.трики верхней части дерева: 7, б, 5, 2 метрики нижней части дерева: 5, 4, 3, 4

Шаг 2: Метрики верхней части дерева: 7, б, 5, б метрики нижней части дерева: 3, б, 1,2.

->0 -1

Рис. 8.2.20. Пример декодирования с обратной связью для свёртотаого юда со скоростью 1/3

Вместо вычисления метрик описанным выше способом, декодер с обратной связью в ДСК можно эффективно реализовать путём вычисления синдрома по принимаемой