последовательности и используя табличный метод коррекции ошибок. Этот метод похож на тот, который был описан выше для декодирования блоковых кодов. Для некоторых свёрточных кодов декодер с обратной связью упрощается к виду, называемому логический декодер по болыттству или пороговый декодер (Месси 1963; Хеллер 1975).

8.2.8, Практические соображения по применению свёрточных кодов

Свёрточные коды широко используются во многих практических приложениях при синтезе систем связи. Декодирование по Витерби предпочтительно используется при малых кодовых ограничениях {К<\, в то время как последовательное декодирование используется при больших кодовых ограничениях, когда сложность декодирования по Витерби становиться чрезмерной. Выбор кодового ограничения диктуется требуемым выигрышем кода.

Из результатов для вероятности ошибки при декодировании мягких решений, данных (8.2.26), очевидно, что выигрыш от кодирования, достигаемый свёрточным кодом, относительно системы без кодирования с двоичной ФМ или КФМ равен

выигрыш от кодирования < 10 lg(7?J.

Мы также знаем, что минимальное свободное расстояние можно увеличить или за счёт уменьшения скорости кода или за счёт увеличения кодового ограничения или тем или другим одновременно. Табл. 8.2.12 дает данные о верхних границах для выигрыша от кодирования для некоторых свёрточных кодов. С целью сравнения табл. 8.2.13 даёт реальные выигрыши от кодирования и верхние границы для некоторых свёрточных кодов с малым кодовым ограничением при использовании декодирования по Витерби. Следует заметить, что выигрыш от кодирования увеличивается по отношению к асимптотическому пределу по мере увеличения ОСШ.

Таблица 8.2.12. Верхние границы вьтгрыша кода для декодировапня мягких решений для некоторых свёрточных кодов

Скорость кода 1/2

Скорость кода 1/3

Рассмотренные результаты базируются на декодировании по Витерби мягких решений. Если используется декодирование жёстких решений, выигрыш от кодирования уменьшается примерно на 2 дБ в канале с АБГШ.

Большие значения выигрыша декодирования, чем те, которые указаны выше в таблицах, достигнуты при использовании свёрточных кодов с ббльшими кодовыми ограничениями, например К = 50 и использовании последовательного декодирования. В любом случае, последовательное декодирование применяется при декодировании жёстких решений для уменьшения сложности устройств. Рис. 8.2.21 иллюстрирует характеристики качества (вероятность ошибки) для некоторых свёрточных кодов с кодовым ограничением К-7 и скоростей кода 1/2 и 1/3 при использовании последовательного декодирования (жёстких решений) и с кодовым ограничением К - 4\ при тех же скоростях кода.

10

10

10-* • L

CKopotrri. 1/3, -А-=41,ПД

Скорости 1 2, А=41.ПД

Скорость 1 2. К-1, Ви гсрби. мягкие решения

Скорость 1/3, А=7, Витерби, мягкие решения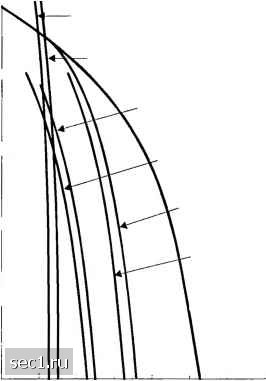

Скорость 1 2, Витерби, жёсткие решения

Скоро».ть 1/3, K-l, Витерби, жесткие решения

Нет кодиропания, ФМ-2

Рис. 8.2.21. Качество при деюдировании по Витерби и последовательном декодировании (ПД) при скорости кода 1/2 и 1/3 [Отига и Levitt (1982). © 19821ЕЕЕ\

Заметим, что при К = А\ код обеспечивает вероятность ошибки 10" при ОСШ 2,5...3 дБ, что на 4...4,5 дБ отличается от предела пропускной способности канала, то есть вблизи предельной скорости. Однако коды с К = 1 и скоростями 1/2 и 1/3 с декодированием мягких решений по Витерби рассчитанные для вероятности ошибки 10, работает при ОСШ соответственно 5 и 4,4 дБ. Эти коды с малым кодовым ограничением достигают выигрыша кодирования примерно 6 дБ при вероятности ошибки 10", в то время как коды с большим кодовым ограничением дают выигрыш около 7,5...8 дБ.

Имеются две важных предпосылки к внедрению декодера Витерби;

1) учёт влияния ограничения интервала обработки, которое будет особенно актуальным при использовании мощных кодов и обеспечит фиксированную задержку декодера;

2) допустимая степень квантования входного сигнала для декодера Витерби.

Исходя из опыта, можно утверждать, что усечение памяти кода на величину пяти кодовых ограничений ведёт к пренебрежимо малым потерям в качестве. Рис. 8.2.22 иллюстрирует качество, полученное при моделировании кода со скоростью 1/2, с кодовым ограничением К = Ъ, 5 и 7 при длине памяти пути 32 бита. В дополнение к усеченной памяти пути, вычисления были сделаны при квантовании входных сигналов, поступающих от модулятора на восемь уровень (3 бита). Штриховые кривые дают результат качества, полученный от верхней границы для вероятности ошибки на бит, даваемой (8.2.26).

3 10- -

10-

Моделирование

Верхняя граница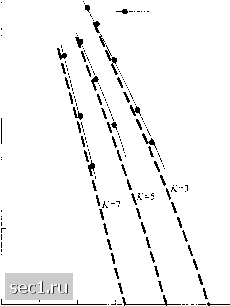

2 3 4 5 6 7

Рис. 8.2.22. Вероятность ошибки на бит ддя кода со скоростью 1/2 при декодировании по Витерби с 8-уровневым квантованием входных сигналов декодера и памятью пути на 32 бита [Heller и Jacobs (1971).© 1971 IEEE]

Заметим, что результаты моделирования близки к теоретической верхней границе, что указывает на то, что ухудшение качества, обусловленное усечением памяти и квантованием входных сигналов декодера, несущественно (0,2...0,3 дБ).

Рис. 8.2.23 иллюстрирует кривые вероятности ошибки на бит для свёрточного кода с = 3... 8, полученные моделированием при декодировании жёстких решений. Заметим, что для кода с = 8 выигрыш от кодирования близок к 4 дБ относительно некодированной КФМ.

Влияние квантования входного сигнала декодера далее иллюстрируются на рис 8.2.24 для кода со скоростью 1/2, К = 5. Заметим, что трехбитовое квантование (восемь уровней) примерно на 2 дБ лучше, чем декодирование жёстких решений, что близко к безусловному пределу, получаемому при декодировании мягких решений в канале с АБГШ.