Пример 8.3.3. Рассмотрим использование сверточного кода со скоростью 1/2, показанного на рис. 8.3.4 (а) для кодирования некоторого информационного символа, в то время как второй информационный символ остается не кодированным.

-о 1

В.\од

(с„С2,Сз) = 000

Некодиропапный бит ( я ) Кодер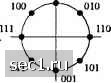

{с) Отображение кодирош1ины.ч

бит {с,. Cj. с,}

в сигнальные точки

а-00

й= 10

с = 01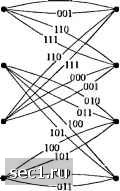

( Ь ) Решётка с 4

СФ-ТОЯНИЯМИ

Рис. 8.3.4. Решётка с 4 состояниями для кодированной модуляции восьмеригаой ФМ

Используем их в объединении с восьми точечным сигнальным созвездием, например, восьми фазовой ФМ или восьми точечной КАМ. Два кодированных символа используются для выбора одного из четырех подобразов сигнального созвездия, в то время как оставшийся информационный символ используются для выбора одной из двух точек внутри каждого подобраза. В этом случае Аг, = 1 и А:, = 1. Решётка с четырьмя состояниями показанная на рис. 8.3.4(й), является в основе своей решёткой для сверточного кода со скоростью 1/2 с добавлением параллельных путей в каждой позиции для размещения

некодированных символов с. Таким образом, кодированные символы {ciyCj)

используются для выбора одного из четырех подобразов, каждый из которых содерхсит две сигнальные точки, а не кодированные символы используются для выбора одной из двух сигнальных точек внутри каждого подобраза. Заметим, что сигнальные точки внутри подобраза удаленны на расстояние = 2л/. Таким образом, расстояние Евклида между

параллельными путями равно d,. Отображение кодовых символов {i,2 з) сигнальными точками иллюстрируется на рис. 8.3.4(c). В качестве альтернативной схемы кодирования мы можем использовать свёрточный кодер со скоростью 2/3 и кодировать 2 информационных символа так, как показано на рис 8.3.5. Это кодирование ведет к решётке с восьмью состояниями и обеспечивает лучшее качество, но требует более сложную реализацию декодера, как описано ниже.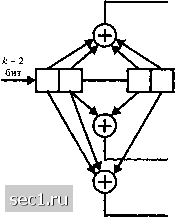

О -It

Рис. 8.3.5. Свёрточный юдер со скоростью 2/3 для кодирования обоих информационных символов

Как блоковый, так и свёрточный коды можно использовать в объединении с расчлененным сигнальным созвездием. В общем, свёрточные коды обеспечивают сравнимый выигрыш кодирования относительно блоковых кодов, а имеющийся в распоряжении алгоритм Витерби приводит к несложной реализации декодирования мягких решений. Из этих соображений мы ограничим наше обсуждение свёрточными кодами (линейными решётчатыми кодами), а в более общем случае (нелинейными) решётчатыми кодами.

Решётчатая кодированная модуляция. Рассмотрим использование сигнального созвездия 8-и уровневой ФМ в объединении с решётчатым кодом. В качестве образца при измерении выигрыша кодирования используем не кодированную четырехфазовую ФМ (4 ФМ). Не кодированная 4 ФМ использует сигнальные точки либо подобраза либо Д на рис 8.3.1, из которого видно, что минимальное расстояние сигнальных точек равно Заметим, что этот сигнал соответствует тривиальной решётке с одним состоянием и четырьмя параллельными переходами состояний, как показано на рис. 8.3.6(a).

Подобразы Dq, Д, и использованы как сигнальные точки с целью

иллюстрации. Для кодированной 8 ФМ модуляции мы можем использовать решётку с четырьмя состояниями, как показано на рис. 8.3.6(6). Заметим, что каждая ветвь решётки соответствует одному из четырех подобразов Q, С,, или . Для восьми точечного созвездия каждый из подобразов Q, С,, и Сз содержит две сигнальные точки. Следовательно, пподобраз С,, содержит две сигнальные точки, соответствующие битам (ООО, 100) или (О, 4) в восьмеричной записи. Аналогично, содержит две сигнальные точки, соответствующие битам (010, 110) или (2, 6) в восьмеричной записи. С, содержит две сигнальные точки, соответствующие битам (001, 101) или (1, 5) в восьмеричной записи и Сз содержит две сигнальные точки, соответствующие битам (011, 111) или (3,7) в восьмеричной записи. Таким образом, каждый переход в решётке из четырех состояний содержит два параллельных пути, как показано более подробно на рис. 8.3.6 (с). Заметим, что любые два сигнальных пути, которые расходятся из одного состояния и сливаются в то же состояние после более одного перехода имеем квадрат расстояний Евклида d-l -f 2i/," = dl +dl между ними.

(а) Решетка о 1 состоянием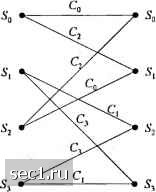

(6) Решйтка с 4 состояниями

Со С, (0.4) (2.6)

С, С, (1.5) (3.7)

С, Со (2.6) (0.4)

С, С, (3.7) (1.5)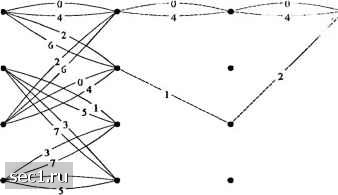

(с) Решётка с 4 состояниями

Рис. 8.3.6. Решётка для некодированной 4ФМ и решётчатый код для сигналов 8ФМ

Для примера, сигнальные пути О, О, О

разделены на

, dl +d; = [(0.765)" + 4]g = 4 .585g. С другой стороны, квадрат расстояния Евклида между

параллельными переходами равно d = 4iS. Следовательно, минимальное расстояние Евклида между путями, которые расходятся из какого либо состояния и сходятся в то же состояние, равно для решётки с четырьмя состояниями d = 2л/. Это минимальное расстояние в решётчатом коде названо свободным евклидовым расстоянием и обозначаются D„.

В решётке из четырех состояний на рис. 8.3.6(6) D=2\!. Если сравнить с

расстоянием Евклида для не кодированной 4 ФМ модуляции, мы видим, что

решётчатый код с четырьмя состояниями дает выигрыш кодирования 3 дБ. Мы хотим подчеркнуть, что решётчатый код с четырьмя состояниями, иллюстрированный на рис. 8.3.6(6), оптимален в том смысле, что он обеспечивает наибольшое свободное Евклидово расстояние. Ясно, можно конструировать много других решётчатых кодов с четырьмя состояниями, включая и тот, который показан на рис. 8.3.7, которые четыре отсчётных перехода из одного состояния до всех остальных состояний. Однако, ни этот код, ни любой из других возможных решётчатых кодов с четырьмя состояниями не даст большее значение Д.

Для решётки с четырьмя состояниями рис. 8-3-6 (б) D - 2л[с] . Если сравнить с

расстоянием Евклида d =42q для некодированной ЧФМ модуляции мы видим, что решётчатый код с четырьмя состояниями даёт выигрыш кодирования 3 дБ.