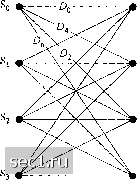Dppp,

Рис. 8.3.7. Альтернативный решётчатый код с 4 состояниями

Конструирование оптимального решётчатого кода с четырьмя состояниями для восьми точечного созвездия было выполнено на основе следуюш;их эвристических правил:

a) параллельные переходы (когда они возникают) назначаются сигнальным точкам, разделенным максимальным расстоянием Евклида, например - 2л[ё для 8 ФМ в четырех подобразах Q, С,, С,, Q.

b) переход, начинающийся и сходящийся в некоторое состояние назначается подобразом (Cq,q) или (С1,Сз), которые имеют максимальное расстояние d = у/тё .

c) сигнальные точки возникают с одинаковой частотой.

Заметим, что правила (а) и (Ь) гарантируют, что Евклидово расстояние связанное с одним и многими путями, которые выходят из определенного состояния и сходятся в это состояние, превосходят Евклидово расстояние для не кодированной 4 ФМ. Правило (с) гарантирует, что решётчатый код будет иметь регулярную структуру.

Хотим указать на то, что специальное отображение кодовых символов в сигнальные точки, как иллюстрировано на рис. 8.3.1, где восемь сигнальных точек представлено в эквивалентную двоичную форму, существенно. Можно разработать ин.1е отображения путём перестановки подобразов таким путём, чтобы сохранить основное свойство -увеличение минимального расстояния среди подобразов.

В решётчатом коде с четырьмя состояниями параллельные переходы разделяются евклидовым расстоянием 2Vi, что тоже равно . Таким образом, вьшгрыш кодирования в 3 дБ ограничивается расстоянием параллельных переходов. Больший выигрыш в качестве относительно не кодированной 4 ФМ можно достичь путём использования решётчатых кодов с большим числом состояний, что позволяет исключить параллельные переходы. Решётчатые коды с восемью или большим числом состояний следует использовать различимые переходы для получения больших значений Д,. Например, на рис. 8.3.8 мы иллюстрируем решётчатый код с восемью состояниями, разработанный Унгербоеком (1982 год) для 8 ФМ сигнального созвездия.

Для максимизации свободного Евклидова расстояния переходы состояний были определены с учетом трех базовых правил, данных выше. В этом случае можно заметить, что минимум квадрата Евклидова расстояния равно

=<+2£/f =4.585,

что, по сравнению с расстоянием d = 2fS для некодированной 4 ФМ представляет выигрыш 3,6 дБ. Унгербоек (1982... 1987) также нашел решётчатые коды со скоростью 2/3 и с 16, 32, 64, 128 и 256 состояниями, которые достигают выигрыш кодирования от 4 до 5,75 дБ для 8 ФМ модуляции.

Dppp, Sj

OpPPi S3

oppp

DppPi s5

OppPa

Dpppi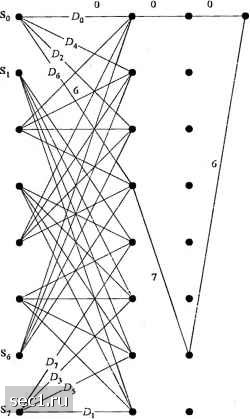

Рис. 8.3.8. Решётчэтый код с 8 состояниями для кодированной модуляции 8ФМ

Базовый принцип расчленения ансамбля легко расширить на большие сигнальные созвездия с ФМ, которые дают большую частотную эффективность. Например, 3 (бит/сТц) можно достичь или не кодированным 8 ФМ или кодированной модуляцией 16 ФМ с решётчатым кодом. Унгербоек (1987) предложил решётчатые коды и рассчитал выигрыш кодирования, достигнутый посредством простых свёрточных кодов со скоростью 1/2 и 2/3 для 16 ФМ сигнального созвездия. Эти результаты суммированы ниже.

Декодирование Витерби мягких решений для решётчато-кодированной модуляции выполняется двумя ступенями. Поскольку каждая ветвь решётки соответствует сигнальному подобразу, то - первая ступень декодирования сводится к определению наилучшей точки сигнала внутри калсдого подобраза, то есть точку в каждом подобразе, которая ближе по расстоянию в к принятой точке. Мы можем это назвать декоОыровситем под образов На второй ступени сигнальные точки, выбранные в каждом подобразе и их метрики квадратов расстояний используются для соответствующей ветви в алгоритме Витерби для определения пути сигнала в кодовой решётке, который имеет минимальную сумму квадратов расстояний от принимаемых сигнальных последовательностей (зашумленный выход канала).

Вероятность ошибки решётчато-кодированных сигналов в присутствии аддитивного гауссовского шума можно рассчитать, следуя процедуре, описанной в разделе 8.2 для свёрточных кодов. Напомним, что эта процедура включает расчет вероятности ошибки для всех различных событий, приводящих к ошибке и к суммированию вероятностей этих событий для получения объединенной верхней границы для вероятности ошибки

декодирования при первом пересечении. Заметим, однако, что при больших ОСШ, вероятность ошибки при первом пересечении в основном определяется лидирующим слагаемым, который имеет минимальное расстояние . Следовательно, при больших ОСШ вероятность ошибки при первом пересечении хорошо аппроксимируется так:

Р. - NO

(8.3.1)

где Nозначает число сигнальных последовательностей с расстоянием Д, которые выходят из определённого состояния и возвращаются в то же состояние после одного или больше переходов.

При вычислении выигрыша кодирования, достигаемого посредством решётчато-кодированной модуляции мы обычно сосредотачиваемся на выигрыш, достигаемый путём увеличения Д и пренебрегаем влиянием N. Однако, решёточные коды с большим числом состояний могут привести к большим значениям Л, что нельзя игнорировать при оценивании всего выигрыша кодирования.

В дополнении к решётчето-кодированной ФМ модуляции, описанной выше, мощные решёточатые коды были также разработаны для сигнальных созвездий AM и КАМ. Особенно важен для практики класс решётчато-кодированных двзхмерных прямоугольных сигнальных созвездий. Рис. 8.3.9 иллюстрирует эти сигнальные созвездия для М-КАМ, где М=16, 32, 64 и 128.

оооооооо оооооооо

о о о о

I °

о о о о

о I I

°!

о о о о о о

о о1 о ООО

о о о

оооо оооо

ооо о о о!оо

II

ооо о о ооо

о о о о о о о о оооооооо

оооооооо оооооооо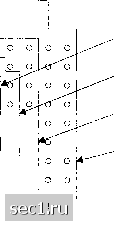

А/ = 32 (крест)

М = б4

Л/= 128 (крест)

Рис. 8.3.9. Прямоугольное двухмерное (КАМ) сигнальное созвездие

Созвездия с М=2 и 128 имеют крестообразные формы и их иногда называют крест созвездиями. Ниже расположенные прямоугольные сетки, содержащие сигнальные точки М-КАМ, названы решётками типа ъ-i (индекс указывает на размерность пространства). Если расчленение ансамбля применить к этому классу созвездий, минимальное евклидово расстояние между последовательными расчленениями равно d-Jd. = V2 для всех /, как мы видели прежде в примере 8.3.2.

Рис. 8.3.10 иллюстрирует решётчатый код с восьмью состояниями, который можно использовать в прямоугольном сигнальном созвездии М-КАМ, М = 2*, где А=4, 5, 6 ... и так далее.