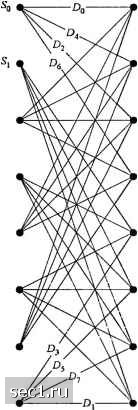Рис. 8.3.10. Решётка с 8 состояниями для прямоугольны. сигнальных созвездий с КАМ

С решёткой из восьми состояний мы связываем восемь сигнальных подобразов так, что подходит любой из Л</-КАМ сигнальных ансамблей при М>\в. Для М = 2™ два входных символа (.= 2) кодируются в и = 3 (w=,+l) символа, которые используются

для выбора одного из восьми состояний, соответствующих восьми подобразам. Дополнительные А-, - - входных символа используются для выбора сигнальных точек внутри подобраза и они приводят к параллельным переходам в решётке из восьми состояний. Таким образом, 16 КАМ включает два параллельных перехода в каждой ветви решётки. В более общем виде, выбор М = 2"*-точечного сигнального созвездия КАМ подразумевает, что решетки с восьмью состояниями содержат 2 параллельных переходов в каждой ветви.

Задание сигнальных подобразов для переходов основьшается на том же наборе базовых (эвристических) правил, описанных выше 8 ФМ сигнального созвездия. Так четыре (ветвевых) переходов, начинающихся от или входящих в то же состояние, задаются подобразами Dg, Д, Д, Д или Д, Д, Д. Параллельные переходы задают сигнальные точки, содержащиеся внутри соответствующих подобразов. Этот решётчатый код с восьмью состояниями обеспечивает выигрыш от кодирования 4 дБ. Евклидово расстояние параллельных переходов превышает свободное евклидово расстояние и, следовательно, качество кода не ограниченно параллельными переходами.

Решётчатые коды с большими размерами для М-КАМ обеспечивают даже большие выигрыши от кодирования. Для примера, решётчатые коды с 2" состояниями для

29-56

М = 2""" сигнального созвездия КАМ можно сконструировать путём свёрточного кодирования входных символов в к+\ выходных символов. Так, для этой цели

используется свёрточный код со скоростью R. = kj {к +1). Обычно выбор к=2

обеспечивает достаточную долю общего достигаемого выигрыша от кодирования. Дополнительные к - т - к входных символов не кодируются, и они передаются в каждом сигнальном интервале, путём выбора символьных точек внутри подобраза.

Таблицы 8.3.1...8.3.3, взятые из статей Унгербоека (1987) дают суммарный выигрыш от кодирования, достигаемый при помощи решётчато - кодированной модуляции Табл. 8.3.1 суммирует выигрыши от кодирования, достигаемые при решётчато-кодированной (одномерной) модуляцией с AM со скоростями решётчатых кодов 1/2. Заметим, что вьшгрыш от кодирования посредством решётчатого кода с 128 состояниями, равен 5,8 дБ для восьми уровневой AM, что близко к предельной скорости канала R и теряет 4 дБ относительно предела пропускной способности канала для частости ошибки в области 10"...10"V Мы можем также видеть, что число путей iV с евклидовым расстоянием становится больше с увеличением числа состояний.

Табл. 8.3,2 показывает выигрыш кодирования для решётчато-кодированной 16 ФМ. Снова видим, что выигрыш кодирования для восьми и более ступеней решётки превышает 4 дБ относительно некодированной 8 ФМ. Простой код со скоростью 1/2 и 128 ступенями решётки дает выигрыш 5,33 дБ.

Табл. 8.3.3 содержит выигрыш кодирования, получаемый решётчато - кодированными сигналами КАМ. Относительно простой решётчатый код со скоростью 2/3 и 128 ступенями решётки дает выигрыш около 6 дБ при т=3 и 4.

Источник: Ungerboek (1987) Таблица 8.3.2. Вьшгрыши кодирования для решётчато-кодироваппых 16-ФМ спгпалов

Таблица 8.3.3. Выигрыши кодирования для решётчато-кодированных КАМ сигналов

Источник: /«егйогЛ-( 1987)

Результаты в этих таблицах ясно иллюстрируют существенные выигрыши кодирования, достигаемые относительно простыми решётчатыми кодами. Выигрыш от кодирования в 6 дБ близок к результату для предельной скорости для

рассматриваемого сигнального ансамбля. Дополнительный выигрыш, который может вести к передаче вблизи границы пропускающей способности канала трудно получить без достаточного увеличения сложности техники кодирования/декодирования.

Поскольку пропускная способность канала определяет окончательный предел качества кодирования, мы можем подчеркнуть, что непрерывное расчленение больших ансамблей сигналов быстро ведет к разделению сигнальных точек внутри некоторого подобраза, что расширяет свободное евклидово расстояние кода. В таких случаях параллельные переходы больше не являются ограничивающим фактором для Д. Обычно расчленение на восемь подобразов достаточно для получения выигрыша кодирования 5-6 дБ при помощи решётчатых кодов со скоростью 1/2 или со скоростью 2/3 с 64 или 128 ступенями решётки, как указанно в табл. 8.3.1...8.3.3. Свёрточные кодеры для линейных решётчатых кодов, иллюстрируемые в табл. 8.3.1...8.3.3 для сигнальных созвездий М-AM, М-ФМ и М-КМЛ даны в статьях Унгербоека (1982... 1987). Кодеры могут быть реализованы с обратной связью или без неё. Например, рис. 8.3.11 иллюстрирует три свёрточных кодера без обратной связи, соответствующие решётчатым кодам с 4,8, 16 состояниями для сигнальных созвездий 8 ФМ и 16 КАМ.

Эквивалентная реализация этих решётчатых кодов, основанная на систематических свёрточных кодерах с обратной связью даны на рис. 8.3.12. Обычно систематические свёрточные кодеры предпочтительны в практических разработках.

Важнейшая проблема для линейных свёрточных кодов заключается в том, что ансамбль модулированных сигналов обычно не инвариантен к изменению фазы. Это ставит проблему в практических разработках, где обычно применяется дифференциальное кодирование, так чтобы преодолеть фазовые флуктуации в случаях, когда приемник должен восстановить фазу несущей после временных ослаблений сигналов. Проблема постоянства фазы и дифференциального кодирования/декодирования была решена Вайем (1984 а,Ь), который изобрел линейные и нелинейные решётчатые коды, которые инварианты к вращению фазы соответственно на 180" или 90". Для примера, рис.8.3.13 иллюстрирует нелинейный свёрточный кодер с восемью состояниями для прямоугольного сигнального созвездия 32-КАМ, который инвариантен к вращению фазы на 90*. Эти решётчатые коды были приняты как международный стандарт для линейных модемов телефонной связи со скоростями 9600 и 14000 бит/с (высокоскоростные).