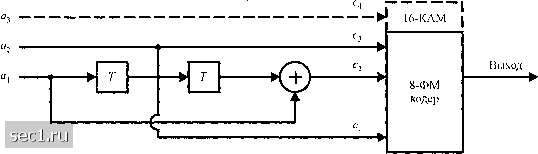(а) Кодер с 4 cocтoянияш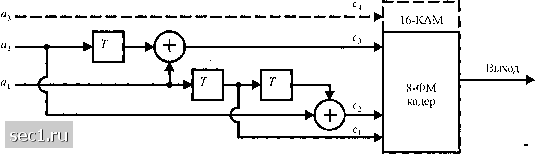

(6) Кодер с 8 состояниями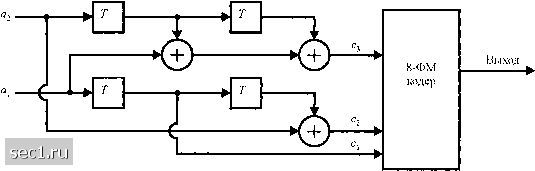

(с) Кодер с 16 состояниями

Рис, 8.3,11. Минимальный кодер без обратной связи для сигналов 8-ФМ и 16-КАМ [Ungerboek (1982), © 1982 IEEE]

Схемы решётчато-кодированной модуляции были также разработаны для многомерных сигналов, В практических системах многомерные сигналы передаются как последовательность или одномерных (AM) или двухмерных (КАМ) сигналов. Решётчатые коды, основанные на 4, 8, и 16 сигнальных созвездий были сконструированы и некоторые из этих кодов были внедрены в имеющиеся в распоряжении коммерческих модемов. Потенциальное преимущество решётчато - кодированных многомерных сигналов заключается в том, что мы можем использовать узко избирательные двухмерные сигнальные созвездия, что позволяет осуществлять выбор между выигрышем кодирования и сложностью реализации. Статьи Вая (1987), Унгербоека (1987), Гершо и Лоуренса (1984) и Форни и др. (1984) трактуют многомерные сигнальные созвездия для решётчато-кодовой модуляции.

-► r -►(+)-► r

(a) Кодер с 4 состояниями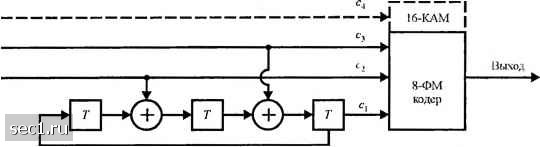

(6) Кодер с 8 состояниями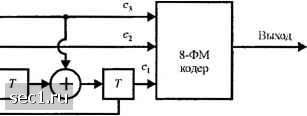

(с) Кодер с 16 состояниями

Рис. 8.3.12. Эквивалентшш реализация систематически.х свёрточных кодов с обратной связью для 8ФМ и 16КАМ [Ungerboek{ШТ). © 1982 1ЕЕЕ\

Наконец мы хотим напомнить, что новая техника синтеза решётчато-кодированной модуляции, основанная на решётках и объединении решёток были описаны Кальдербанком и Слозном (1987) и Форни (1988). Это метод конструирования решётчатых кодов обеспечивает альтернативу методу расчленения ансамблей, описанному выше Однако, эти два метода тесно связаны. Этот новый метод привёл к открытию новых мощных свёрточных кодов, включающих большие сигнальные созвездия. Многие из них приведены в статье Кальдербанка и Слоэна (1987).

8.4. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ

Пионерские работы по кодированию и кодированным сигналам для цифровой связи были сделаны Шенноном (1948а, Ь), Хеммингом (1950) и Голеем (1949). За этими работами скоро последовали статьи по качеству кодирования Гильберта (1952), по новым кодам Маллера (1954) и Рида (1954) и по технике кодирования для каналов с шумами Элиаса (1954... 1955) и Слепяна (1956).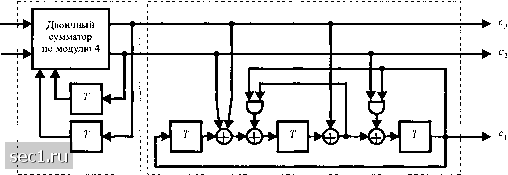

Дифференциальный кодер

Нелинейный свёрточный кодер (а) Кодер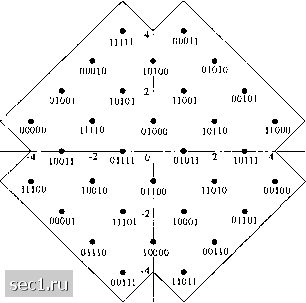

Дв011чная по следовательно сть, отображаемая синальной точкой: Cj С3 С2 с-

(6) 32-точечный КАМ сигнал (крест)

Рис. 8.3.13. Нелинейный свёрточный кодер с 8 состояниями для сигнального ансамбля 32-КАМ, который проявляет инвариантность к повороту фазы на 90°

В течение периода 1960... 1970 появился целый ряд существенных вкладов в развитие теории кодирования и алгоритмов декодирования. В частности, мы цитировали статьи Рида и Соломона (1960) и коды Рида-Соломона, статьи Хоквингема (1959) и Боуза и Роя-Чоудхурн (1960 а, Ь) по БЧХ-кодам и диссертация на степень доктора философии Форни (1966 а) по каскадным кодам. За этими работами последовали статьи Гоппа (1970, 1971) по конструированию нового класса линейных циклических кодов, теперь называемые кодами Гоппа (смотри также Берлекэмп, 1973) и статьи Джастисена (1972) по конструктивной технике асимптотически хороших кодов. В течение этого периода работы по асимптотике декодирования были первоначально сфокусированы на БЧХ коды. Первый алгоритм декодирования для двоичных БЧХ кодов был разработан Питерсоном (1960). Большое число утончённых разработок и обобщений Чайна (1964), Форни (1965), Мэсси (1965) и Берлекемма (1968) вели к разработке эффективных в вычислительном отношении