
 | |
|
НПО Системы Безопасности (499)340-94-73 График работы: ПН-ПТ: 10:00-19:00 СБ-ВС: выходной  |
Главная » Периодика » Безопасность 0 ... 145146147148149150151 ... 262 алгоритмов декодирования БЧХ кодов, которые детально описаны Лином и Костелло (1983). Параллельно с этими разработками по блоковым кодам шли разработки свёрточных кодов, которые были открыты Эллиасом (1955). Важнейшая проблема свёрточных кодов -их декодирование. Возенкрафт и Райфен (1961) описали алгоритм последовательного декодирования для свёрточных кодов. Этот алгоритм был позже модифицирован и уточнен Фано (1963) и теперь он называется алгоритмом Фано. Впоследствии были изобретены стек-алгоритмы Зигангировым (1966) и Елинеком (1969), а алгоритм Витерби был открыт Витерби (1967). Оптимальность и умеренная сложность при малых кодовых ограничениях способствовали тому, что алгоритм Витерби стал наиболее популярен для декодирования свёрточных кодов с кодовым ограничением ЛГ< 10. Одним из наиболее важных вкладов в кодирование в течение 70-х годов были работы Унгербоека и Чайка (1976) по кодированию в ограниченных по полосе каналах. В этих статьях было показано, что можно достичь достаточный выигрыш кодирования путём введения избыточности в сигнале при ограниченном по полосе канале и были предложены решётчатые коды, достигающие выигрыш кодирования порядка 3-4 дБ. Эта работа вызвала большой интерес среди исследователей и привела к большому числу публикаций за последние 10 лет. Много ссылок можно найти в статьях Унгербоека (1982, 1987) и Форни и других (1984). Дополнительные статьи по кодированной модуляции для ограниченных по полосе каналов можно найти в «SpecJal Issue on Voiceband Telephone Data Transmission, IEEE Journal on Selected Areas in Communication)) (September 1984). Всесторонняя трактовка решётчато-кодированной модуляции дана в книге Биглиери и др. (1991). Дополнительно к ссылкам, данным выше по кодированию, декодированию и синтезу кодированных сигналов, мы хотим вспомнить коллекцию статей, опубликованных в IEEE Press и озаглавленных «Кеу Papers in the Development of Coding Theory)), изданных Берлекэмпом (1974). Эта книга содержит важные статьи, которые были опубликованы в первые 25 лет развития теории кодирования. Мы хотим также процитировать Special Issue on Error - Correcting Codes, IEEE Transactions on Communication (октябрь 1971). ЗАДАЧИ 8.1. Дана порождающая матрица линейного б.локового двоичного кода. Го О 1 1 1 О Г О 1 О О 1 1 1 10 0 1110 a) выразите G в систематической форме lp]. b) определите проверочную матрицу Н для кода. c) сконструируйте таблицу синдромов для кода. d) определите минимальное расстояние кода. e) покажите, что кодовое слово, соответствующее информационной последовательности 101, ортогонально к Н. 8.2. Напишите кодовые слова, генерируемые матрицами, данными в (8.1.35) и (8.1.37) и затем покажите, что эти матрицы генерирует одинаковый ансамбль кодовы.ч слов. 8.3. Распределение весов кодов Хемминга известно. Выраженное в виде полинома степеней х распределение весов двоичного кода Хемминга с длиной блока п имеет вид А(х)=Уа,х =-{1 + хУ +n{l + xf- {l-xf" где А, - число кодовы.ч слов с весом /. Используете эту формулу для определения распределения весов кода Хемлшнга (7.4) и сравните ваш результат со списком кодовы.\ слов, данном в табл. 8.1.2. 8.4. Полином g{p) = p + p+ является порождающим для двошого кода Хемминга (15, 11), a) определите порождающею матрицу G д.та этого кода в систематической форме. b) определите порождающею матрицу для дуального кода. 8.5. Для циклического кода Хемминга (7, 4) с порождающим полиномом сконструируйте расширенный код Хемминга (8, 4) и приведите список кодовы.х слов. Каково rf,,,,,, дая расширенного кода(?). 8.6. Линейный блоковый код (8, 4) сконструирован укорочением кода Хемминга (15, 11), генерированного порождающим полиномом g{p)=P+P + - a) Сконструируйте кодовые слова для кода (8, 4) и дайте их список. b) Каково минимальное расстояние кода (8, 4)? 8.7. Факторизация полинома р +1 даёт +1=(р+р+iip+p+р-+p+i){p+p+ijp-+p+i\p+i). a) сконструируйте систематический код (15, 5), использующий порождающий полином g{p)={p* + Р + Р + P + + P + + b) Каково минимальное расстояние кода? c) Сколько случайных ошибок в кодовом слове можно исправить? с1) Сколько ошибок можно обнаружить кодом? с) Напишите кодовые слова кода (15, 2), сконструированного порождающим полиномом и определите его минимальное расстояние. 8.8. Сконструируйте проверочные матрицы Н, и Н, соответствующие порождающим матрицам G, и Gt , данные, соответственно, (8.1.34) и (8.1.35). 8.9. Сконструируйте расширенный код (8,4) из кода Хемминга (7.4) путём видоизменения порождающей и проверочной матриц. 8.10. Систематический код (6, 3) имеет проверочную матрицу 1 0 0 11 о" G= О 1 О О 1 1 0 0 110 1 Cкoнcтpиpyйтe стандартное расположение и определите корректируемые образцы ошибок и соответствующие им синдромы. 8.11. Сконструируйте стандартное расположение для кода (7, 3) с пороледающей матрицей 1 О О 1 О 1 Г G= О 1 О 1 1 1 О 0 0 10 111 и определите корректируемые образцы ошибок и соответствующие им синдромы. 8.12. Определите корректируемые образцы ошибок (с наименьшим весол и их синдромы для цшслического кода Хемминга (7, 4). 8.13. Докажите, чго если сумма двух образцов ошибки е, и Ст является действительным кодовым словом , то каждый образец ошибки имеет одинаковый синдром. 8.14. Пусть g{p)=p+p+p+p+l является полиномом относительно двошого по.та. a) найдите циклический код с наименьшей скоростью, для которого порождающим полиномом яв.тяется g{p). Какова скорость этого кода? b) найдите минимальное расстояние кода, найденного в (а). c) каков вьшгрыш кодирования д.та кода найденного в (а). 8.15. Рассматривается полином g{p)= р + 1 относительно двoишoгo поля. a) покажите, что этот полином может генерировать гщклический код при любом выборе п. Найдите соответствующее значение к. b) найдите систематическую форму G и Н для кода, генерируемого посредством g{p). c) можете ли сказать, какого типа код создается этим порождающим полиномом? 8.16. Синтезируйте циклический код (6, 2) выбором возможно короткого порождающего полинома. a) определите порождающую матрицу G (в систематической форме) для этого кода и найдите все возможные кодовые слова. b) сколько ошибок может корректировать этот код? 8.17. Докажите, что суммирование любььч двух комбинаций в одной строке стандартного расположения даёт возможное кодовое слово. 8.18. Исходя из БЧХ кода (15, 7), сконструируйте укороченный код (12, 4). Дайте порождающую матрицу дтя укороченного кода. 8.19. В разделе 8.1.2 было указано, что когда код Адамара {п,к) отображается в сигналы посредством дв0и1ш0й ФМ соответствующие А/ = 2* сигналов ортогональны. Определите показатель расширения полосы для Л/ ортогональных сигналов и сравните с требованиями по полосе для ортогональных сигналов ФМ при когерентном детектировании. 8.20. Покажите, что сигналы, генерируемые кодом регистра сдвига максимальной длины при отображении каждого кодового символа в кодовом слове двоичным ФМ сигналом одинаково коррелированны с коэффициентом корреляции р, =-1/(M-1), то есть Л/сигналов образует симплексный ансамбль. 8.21. Вычислите вероятность ошибки декодирования, получаемой в канале с АБГШ при использовании кода Хемминга (7, 4) при декодировании жёстких и мягких решений. Используйте (8.1.50), (8.1.52), (8.1.82), (8.1.90) и (8.1.91). 8.22. Используйте результаты раздела 2.1.6 полученные для фаницы Чернова при декодировании жёстких решений (формулы (8.1.89) и (8.1.90)). Предположив, что передано кодовое слово из одних нулей, определите верхнюю границу для вероятности того, что выбрана декодером кодовое слово С„, имеющий вес . Это имеет место, если w„, или больше символов принято с ошибкой. Для определения границы Чернова определите последовательность из случайных вели1шн, как с вероятностью р, с вероятностью \ - р, где i = 1,2.....w„, а /? - вероятность ошибки в канале. Ддя ДСК величины {Л,} статистически независимы. 8.23. Свёрточный код описывается генераторами g.=M 82=[l0lJ 8з=М a) получите кодер, соответствующий этому коду, b) получите диаграмму состояний для этого кода, c) получите решётчатую диафамму для этого кода, (1) найдите передаточную функцию и свободное расстояние этого кода, е) проверьте, является ли этот код катастрофическим. 8.24. Свёрточный код из задачи 8.23 используется для передачи по каналу с АБГШ при декодировании жёстких решений. Выходом детектора (демодулятора) является (101001011110111...). Используя алгоритм Витерби, найдите переданную последовательность. 8.25. Повторите задачу 8.23 для кода с генераторами g.=[ll0lg2-[l04g3=[llll 8.26. Блок-схема двоичного сверточного кодера показана на рисунке Р8.26. a) Получите диафаммы состояний кода. b) Найдите передаточную функцию кода T(D). c) Каково минимальное свободное расстояние кода d? d) Предположите, что сообщение кодируется этим кодом и передается через двоичный симметричный канал с вероятностью ошибки /> = 1. Используя алгоритм Витерби найдите переданную последовательность символов, если принята последовательность Рис. Р8.26 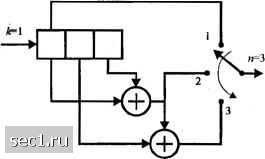 0 ... 145146147148149150151 ... 262 |