r = (llO, 110, 110, 111, 010, 101, lOl).

e) Найдите верхнюю границу для вероятности ошибочного декодирования, если используется указанный выше двоичный симметричный канал. Сделайте приемлимую аппроксимацию. 8.27. Блок схема свёрточного кода (3, 1) показана на рисунке Р8.27.

a) Получите диаграммы состояний кода.

b) Найдите передаточную функцию кода T{D) .

c) Найдите минимальное свободное расстояние

кода (йсв) и покажите соответствующий путь (на

расстоянии с/сЕ относительно кодового слова из одних нулей) на решётке.

(1) Предположите, чго четыре двоичны.\

информационных символа (х, х, х, х, за

которыми следуют два нуля закодированы. Эта информация передается по двоичному симметричном) каналу с переходной вероятностью ошибки О, 1 Принимаемая последовательность такова (111, 111, 111, 111, 111, 111). Используйте алгоритм декодирования Витерби, чтобы найти переданную последовательность данных.

8.28. Для свёрточного кода, генерируемого кодерол, показанным на рисунке Р8.28:

a) Найдите передаточную функцию кода в форме

t{n,d)

b) Найдите свободное расстояние кода dec-

c) Найдите верхнюю границу для средней вероятностной ошибки на бит, используя границу для вероятности ошибочного декодирования жёстких решений, если код используется в канале при условии, что переходная вероятность ошибки в

Рис. Р8.27

1с=1

\ g2=[nO]

Рис. Р8.28

канале р = 10

8.29. На рис. Р8.29 изображён свёрточный код со скоростью 1/2 и кодовым ограничением К=2

Входная

двоичная ►

по следовательно сть

У>. Выходная

► двоичная последовательность

Рис. Р8.28

a) Нарисуйте древовидную диаграмму кода, решётчатую диаграмму и диаграмму состояний.

b) Найдите передаточною функцию T(N,0,У) и по ней определите минимальное свободное расстояние.

8.30. На рисунке Р.8.30 показан свёрточный код со скоростью 1/2, К=3:

a) Получите дерево кода, диаграмму решётки и диаграммы состояний.

b) Определите передаточную функцию t{N,D,j) и с ее помощью найдите минимальное свободное расстояние.

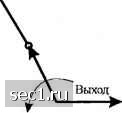Рис. R8.30

8.31. Нарисуйте схемы свёрточных кодеров по следующим параметрам:

a) Скорость кода 1/2, К=5, максимальное свободное расстояние (табл. 8.2.1).

b) Скорость кода 1/3, К=5, максимальное свободное расстояние (табл. 8.2.2).

c) Скорость кода 2/3, К=2, максимальное свободное расстояние (табл. 8.2.8).

8.32. Получите диафамму состояний для сверточного кода со скоростью 2/3, К=5, указанных в задаче 8.31(c) и покажите для каждого перехода выходную последовательность и расстояние вы.ходной последовательности от последовательности состоящей из одних нулей.

8.33. Рассмофите свёрточный код со скоростью 1/2, К=3, показанный на рисунке Р8.30. Предположим, что код используется в двоичном симмефичном канале и принимаемая последовательность для первых восьми ветвей такова 0001100000001001. Посфойте диафамму рещётки. Проследите за решением по диафамме решётки и пометьте у выживших путей расстояние Хемминга на каждом узле. Если возникнет неувязка с мефиками, фебуемыми для решения, выберете верхний путь (произво.льный выбор).

8.34. Используйте передаточную функцию, полученную в задаче 8.30 для сверточного кода со скоростью Rc=\l2, К-3, для расчета вероятности ошибки на бет в канале с АБГШ при декодировании жёстких решений (а) и мягких решений (Ь). Сравните качество, построив результаты расчетов на одном фафике.

8.35. Используйте генераторы, данные (8.2.36) для получения кодера для функции 3-дуального сверточного кода со скоростью 1/2. Определите диафамму состояний и получите передаточную функцию

t(n,d,j).

8.36. Получите диафамму состояний для сверточного кода, генерируемого кодером, показанным на рисунке Р8.36 и затем определите является ли код катасфофическим или нет. Также дайте пример сверточного кода со скоростью 1/2, К=4, который проявляет катастрофические распространения ошибок.

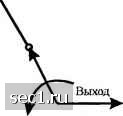Рис. R8.36

8.37. Решётчато-кодированный сигнал формируется так, , как показано на рисунке Р8.37 путем кодирования одного символа посредством сверточного кода со скоростью 1/2 а три дополнительных

информационных символа остаются некодированными. Образуйте расчленение ансамбля созвездия 32КАМ (крест) и укажите подобразы в расчленении. Насколысо увеличится расстояние между соседними сигнальными точхсами в результате расчленения?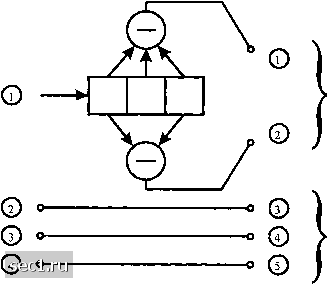

Кодированные биты

Некодирова1Шые биты

Рис. R8.37

8.38. Пусть Xl и Аг - два кодовых слова длины п с расстоянием d и предположите, что эти два кодовых слова передаются по двоичному симметричному каналу с переходной вероятностью ошибки р. Пусть Р(с1) обозначает вероятность ошибки при передаче этих кодовых слов.

а) Покажите, что

2"

где суммирование ведется по всем двoишым последовательностям у, Ь из вышесказанного заключите, что

P{d)<[4p{l-p)