где x{t) - отклик фильтра на приёме на входной импульс /;(/), а v(/) - отклик фильтра на шум z(/)

Теперь, если y{i) стробнруется во времени в точках t кТ + т, к = 0,\,..., мы имеем

y{kT+XQ)-y,=flAfT-riT + x,)+v{kT + x,), (9.2.5)

.;=0

ИЛИ, что эквивалентно

Л=ЕЛп+. = 0,1,...,

(9.2.6)

где Xq- задержка при передаче по каналу. Величины отсчетов можно выразить так

xq п=0

+ V,, Л: = 0,1,....

(9.2.7)

Мы считаем произвольным (известным) скалярным множителем, который, для удобства, примем равным единицы. Тогда

-/.+S/A-„+v,. (9.2.8)

Слагаемое 7. представляет желательный информационный символ в к-й отсчетной точке, слагаемое

пк-п

представляет межсимвольную интерференцию (МСИ), а v. - аддитивная гауссовская

шумовая величина в -ой отсчетной точке.

Уровень МСИ и шум в цифровых системах связи можно наблюдать на осциллографе. Для сигналов AM мы можем наблюдать принимаемый сигнал y{t) на вертикальном входе (по вертикальной оси) при периоде горизонтальной развёртки, кратном Т. Результирующая осциллограмма на дисплее называется глазковой диаграшюи из-за её сходства с человеческим глазом.

Для примера, рис.9.2.1 иллюстрирует глазковую диаграмму для двоичной и четырехуровневой AM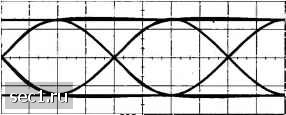

двоичная

4-позиционная

Рис. 9.2.1. Примеры глазковых диаграмм для двоичной и 4-позиционной AM

Влияние МСИ проявляется в закрытии глазка, тем самым уменьшается допуск на величину аддитивного шума, вызывающую ошибку. Рис. 9.2.2 графически иллюстрирует

46-;

влияние МСИ на сокращение открытости двоичного глазка.

Оптимальное время

Чувствительность отсчёта Искажения

к ошибкам синхронизации

переходов через нуль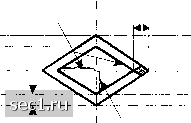

Размах искажений Допуск для шума

Рис. 9.2.2. Влияние МСИ на раскрытие глазковой диаграммы

Заметим, что МСИ искажает положение переходов через нуль и вызывает уменьшение открытости глазка. Тем самым она обуславливает большую чувствительность системы к ошибкам временной синхронизации.

Для ФМ и КАМ привычно рассматривать «глазковую диаграмму» как двухмерную диаграмму рассеяния, иллюстрирующая величины отсчетов (у,, }, которые представляют

величины решений в отсчётных точках. Рис. 9.2.3 иллюстрирует такую глазковую диаграмму для сигнала 8 ФМ.

Переда1шьп1 Отсчеты сигнала 8-фазыый на выходе

сигнал демодулягора

(а) (а)

Рис. 9.2.3. Двухмерные цифровые глазковые диах-раммы

В отсутствие МСИ и шума переданный сигнал в отсчётные моменты времени порождает в месте приёма восемь различимых точек, соответствующих восьми переданным значениям фаз сигнала. МСИ и шум приводят к отклонению принимаемых отсчетов {у} от лселаемых сигналов 8 ФМ. Чем больше МСИ и шум, тем больше

рассеяние отсчетов принимаемых сигналов относительно точек передаваемых сигналов

Ниже мы рассмотрим проблему синтеза сигналов при условии, что в отсчётных точках нет МСИ

9.2.1. Синтез ограниченных по полосе сигналов при отсутствии межсимвольной интерференции - критерий Найквиста

В этом разделе и в 9.2.2 мы предположим, что ограниченные по полосе каналы имеют идеальную частотную характеристику, т.е. С(/) = 1 для / < Ж, Тогда импульс x{t) имеет

спектральную характеристику Jf(/)= G(/)" , причём

(9.2.9)

Мы интересуемся спектральными свойствами импульса x{t) и затем передаваемого импульса g(t), когда нет межсимвольной интерференции. Поскольку

Л (9.2.10)

,1-0

то условие отсутствия МСИ можно записать так

x{t = kT)x,4 (9.2.11)

\0(A;t0).

Ниже мы определим необходимые и достаточные условия для X(J) для того, чтобы импульс х{() удовлетворял бы вышеуказанному соотношению. Это условие известно, как критерий отсчётности сигнала Найквиста или условие Найквиста для нулевой МСИ. Оно формулируется следующей теоремой.

Теорема (Найквиста). Необходимое и достаточное условие для того, чтобы x{t) удовлетворяло условиям

x(«r) = f "" (9.2.12)

[о (и;0)

сводится к тому, чтобы преобразование Фурье X(J) удовлетворяло условию

X{f + mlT) = T. (9.2.13)

Доказательство.

В общем х(г) определяется обратным преобразование Фурье X(J). Следовательно,

x(t)=r X{J)edf. (9.2.14)

, J-00

В точках отсчета / = пТ это соотношение принимает вид

x(nT) = lXif)e df. (9.2.15)

Разобьем интеграл в (9.2.15) на интегралы, перекрывающие ограниченные области частот 1/Г. Тогда получаем

-(«п= S г;;; xu)-df= ix{f+miT).-df=

m=-a> m=-ai

= С Т)] е--" V/ = III Bif) е-> V/,

Lm--a>

где мы определили B{f) так:

B{f)=±X{f + mlT). (9.2.17)

m=-oo

Очевидно, что 5(/) является периодической функцией с периодом 1/7" и, следовательно, ее можно представить рядом Фурье

K = T\Zr(f)df. (9.2.19)