Сравнив (9.2.19) и (9.2.16) находим

Ь„=Тх{-пТ). (9.2.20)

Следовательно, достаточное и необходимое условие для (9.2.11) сводится к тому, что

, ГГ (« = 0)

*„=1 (9 2 21)

" [О («0). к..ч

Подстановка этого условия в (9.2.18) дает

В(Л = Т (9.2.22)

или, что эквивалентно

j;X(f + m/T) = T.

(9.2.23)

Этим заканчивается доказательство теоремы.

Теперь предположим, что канал имеет полосу W. Тогда С(/) = 0 для />Жи, следовательно, Х(/) = О для \f\>W. Мы рассмотрим три случая.

1. Когда T<]/2W или, что эквивалентно l/T>2W. Поскольку 5(/)= Y,X(f + n/T)

состоит в этом случае из неперекрывающихся копий Х(/), разделенных интервалом l/T, как показано на рис. 9.2.4, то нет возможности выбрать X(f) так, чтобы удовлетворить условию B(f) = Т ,и таким путем мы не сможем синтезировать систему без МСИ.

5(/)=Zx(/+wr)

-1 -+w-w

Рис. 9.2.4. Кривая B(f) для случая T<mF

2. Когда T = l/2W или, что эквивалентно, \/T = 2W (скорость Найквиста), повторения X{f), разделенные интервалом l/T, показаны на рис. 9.2.5. Ясно, что в этом случае существует только одна характеристика X(J), которая удовлетворяет условию В{/) = Т, именно

т (/<г)

О при других /.

Х(Л = \

(9.2.24)

что ведёт к импульсу

sm(%t/T) .

x(t) = -- = sine

ntlT

(9.2.25)

Это значит, что наименьшее значение Г, при котором возможна передача с нулевой МСИ, это Т = 1/2W, и при этом условии x{t) является функцией sine. Трудности такого выбора функции x{t) заключаются в том, что она некаузальная и, следовательно, не реализуемая.

-л /

\гтлг-

1 т

о iv=mT

Рис. 9.2.5. Кривая B(f) для случая T=U2F

Чтобы сделать её реализуемой, обычно вводят задержку, т.е. используется функция sinc[7t(/-/o)/r], а /(, выбирается так, чтобы при /<0 иметь 81Пс[я(/-/(,)/Г]иО. Конечно,

при таком выборе x(t) время стробирования также надо сдвигать до тТ+1. Вторая

трудность с такой огибающей импульса заключается в том, что скорость её сходимости к нулю медленная. «Хвосты» от х(/) затухают, как \/Т, следовательно, малая ошибка в моменте взятия отсчёта на выходе согласованного фильтра демодулятора ведет к неограниченному ряду компонент МСИ. Такой ряд абсолютно не сходится из-за низкой скорости затухания импульса l/Г и, следовательно, результирующая МСИ в принципе не сходится.

3. Когда Т >\l2W, то B(J) состоет из перекрывающихся копий X{f), разделенных интервалом XJT, как показано на рис. 9.2.6. В этом случае существует несчётное число выборов Х(/), при которых В(/)=Т.

. S(/)=Ix(/n<Г) i V n=to

X ; ,Х, i ,Х

Рис. 9.2.6. Кривая B(J) для случая Т> 1/2F

Частный спектр импульса для случая T>\/2W, который имеет требуемые спектральные свойства и который широко используется на практике-это спектр приподнятого косинуса. Частотная характеристика приподнятого косинуса (см. задачу 9.11) определяется так:

ХМ) =

о</ Г1-Р

1 + р-2Т

(9.2.26)

где Р называется коэффициентом ската и принимает значение в области О < Р < 1. Полоса, которую сигнал занимает вне полосы Найквиста 1/2Г, называют излишком полосы, и он

обычно выражается в процентах от полосы частот Найквиста. Например, если 3 = , излишек полосы равен 50%, а когда р = 1, излишек полосы равен 100%. Импульс x{t), имеющий спектр приподнятого косинуса, определяется так:

МНт-Мт = ,,„,(„/г)5*. (9.2,27)

Заметим, что x{t) нормирован так, что х(0) = 1. Рис. 9.2,7 иллюстрирует спектральные характеристики приподнятого косинуса и соответствующие импульсы для Р = О, и 1.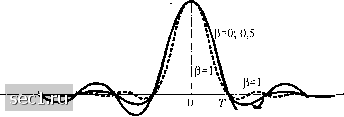

IT ЗГ (а) Р=0 р=о5

AT t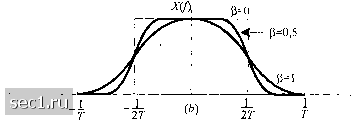

Рис 9.2.7. Импульсы, имеющие спектр типа приподнятого косинуса

Заметим, что при Р = О импульс вырождается в x(t) = sine {nt IT), a скорость передачи символов равна \/T = 2W. Если р = 1 скорость передачи символов \/T = W. В общем, хвосты x{t) убывают как \/t для Р>0. Следовательно, ошибка при стробировании отсчётов ведет к ряду компонент МСИ, который сходится к конечной величине.

С учетом «гладкостных» характеристик спектра приподнятого косинуса возможно синтезировать реализуемые фильтры для передатчика и приёмника, которые аппроксимируют желательные суммарные частотные характеристики. В частном случае, когда канал идеален, т.е. С(/) = 1, \f\<W, имеем

XM) = G,(f)G,(f), (9.2.28)

где Gj.(f) и G(/) - частотные характеристики двух указанных фильтров. В том случае, когда фильтр на приёме согласован с фильтром на передаче, имеем

XM) = Grif)G,(f) = \GAf)t

В идеале

Gr(f)-yl\xJn\\ (9.2.29)

и Gjf(f) = G(f), а /(,- некоторая номинальная задержка, которая должна удовлетворить

физической реализуемости фильтра. Таким образом, суммарная спектральная характеристика приподнятого косинуса расщепляется поровну между фильтрами передатчика и приёмника. Подчеркнем также, что необходима дополнительная задержка для обеспечения физической реализуемости фильтра на приёме: