9.2.2. Синтез ограниченных по полосе символов с контролируемой МСИ -сигналы с парциальным откликом

Как мы видели из нашего обсуждения синтеза сигналов, для получения нулевой МСИ необходимо сократить скорость передачи символов l/Г ниже скорости Найквиста 2W символов/с для практической реализации фильтров на передаче и приёме. С другой стороны, предположим, что мы снимем требование нулевой МСИ и, таким образом, достигнем скорости передачи символов 2W символов/с. Допуская контролируемую величину МСИ, мы можем достичь эту скорость передачи символов.

Мы уже видели, что условием для нулевой МСИ является х(пТ) = о для пО. Однако предположим, что мы синтезируем ограниченный по полосе сигнал с контролируемой МСИ в определённый момент времени. Это означает, что мы допускаем некоторую дополнительную ненулевую величину МСИ в отсчётах {х(пТ)}, которую мы вводим. Она детерминирована или «контролируема» и может принять определённую величину в приёмнике, что обсудим ниже.

Один частный случай, который ведет (приближённо) к физически реализуемым фильтрам передатчика и приёмника, определяется нормированными отсчетами

fl (« = 0, 1) [о (при других «). Теперь, используя (9.2.20), мы получим

\Т (« = 0,-1) [о (при других /?), что, при подстановки в (9.2.18) дает

5(/) = Г + 7е-. (9.2.32)

Как и в предыдущем разделе, невозможно удовлетворить этому уравнению при Т < \/2W. Однако для Г = \J2W мы получим

х{пТ) = .

Ъ. =

(9.2.30)

(9.2.31)

Х(Л =

-(l + e-") t\<w) 2W /V /

-e cos- W

y\<w)

2Ж (9.2.33)

(при других /).

О (при других /)

Следовательно, x(t) определится так

x(t) = sinc(27iH/)+sinc[2jr(l/ - )]. (9.2.34)

Этот импульс называется дуобинарным сигнальным импульсом. Он иллюстрируется вместе со спектром амплитуд на рис. 9.2.8.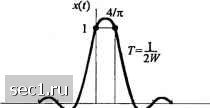

J- cos

-37" -IT-T О Т ТГЪТ AT t -W W f

Рис. 9.2.8. Характеристика во временной и частотной областях дуобинарного сигнала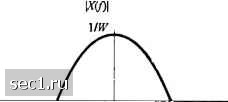

Удобно иметь дело с отсчетами x{f), которые нормированы к единице для и = 0,1.

Заметим, что спектр падает до нуля плавно, что означает, что можно синтезировать физически реализуемые фильтры, которые аппроксимируют этот спектр очень плотно. Таким образом достигается скорость передачи 2W .

Другой частный случай, который ведет (приближенно) к физически реализуемым фильтрам передатчика и приёмника, определяется отсчётами

1 (п = -\)

= х(пТ) =

-1 (,, = 1) о при других п.

(9.2.35)

Соответствующий импульс х(/) определяется так:

х(/) = sine

а его спектр

2W W

-sin- W

f\<W f >w.

(9.2.36)

(9.2.37)

Этот импульс и его спектр амплитуд иллюстрируются на рис. 9.2.9. Он называется модифицированным дуобинарным импульсом сигнала. Интересно отметить, что спектр этого сигнала равен нулю при / = о, что делает его подходящим для передачи по каналу, который не пропускает постоянную составляющую.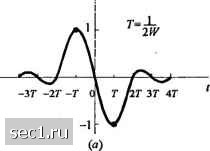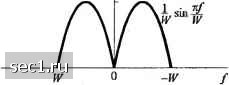

Рис. 9.2.9. Характеристика во временной и частотной областя.\ модифицированного дуобинарного сигнала

Можно получить другие интересные и физически реализуемые характеристики фильтров, как показано Кречмером (1966) и Дакки и др. (1968), выбирая различные значения для отсчетов [x{nl2W)} и больше, чем два ненулевых отсчета. Однако, если мы

выберем больше ненулевых отсчетов, то проблема отслеживания контролируемой МСИ становится более трудной и практически неразрешимой.

В общем, класс ограниченных по полосе импульсов сигналов, имеющих форму

г-"/ "

\2W)

(9.2.38)

и соответствующий спектр

2W, О

i\f\<w) y\>w)

(9.2.39)

называют сигналами с парциальным откликом, когда контролируемая МСИ намеренно вводиться отбором двух или больше ненулевых отсчетов из ансамбля {x(n/2W)}. Результирующий сигнальный импульс позволяет нам передавать информационные символы со скоростью Найквиста 2W символов/с. Детектирование принимаемых символов в присутствии контролируемой МСИ описывается ниже.

Альтернативное представление сигналов с парциальным откликом. Мы включили этот подраздел для представления других интерпретаций сигналов с парциальным откликом. Предположим, что сигнал с парциальным откликом генерируется так, как показано на рис. 9.2.10, путём прохождения последовательности {/„}с дискретным временем через линейный фильтр с дискретным временем и с коэффициентами

=x{ri/2W), w = 0,1,N-l и использовании выходной последовательности {BJ этого

фильтра для периодической подаче ... на аналоговый фильтр с импульсной характеристикой smc{2KWt).

S I«50 пТ)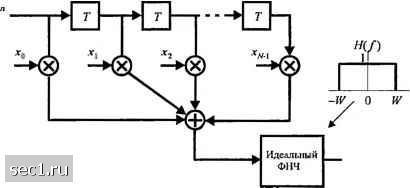

Б В„5(/-лГ)

Выход

Рис. 9.2.10. Альтернативный метод формирования сигаала с парциальным откликом

Результирующий выходной сигнал фильтра идентичен сигналу с парциальным откликом (9.2.38) Поскольку

B„ = Y.4h,, (9.2.40)

то последовательность символов {В) коррелированна вследствие фильтрации последовательности (/„}. Действительно, автокорреляционная функция последовательности {В„} равна

Ы \N-\

ф(/«) = E{B„B„J = SZ./(C./„.™-,)

(9.2.41)

<r=0 /=0

Когда входная последовательность имеет нулевое среднее и равномерный спектр, то

ДСЛ.«-,) = 5„,, „ (9.2.42)

где мы использовали нормирование £(/) = 1. Подстановка (9.2.42) в (9.2.41) приводит к

желательной автокорреляционной функции {В) в виде

JV-l-H

ф(/я)= 2 Л.И " = 0,±1,...,±(Л-1). (9.2.43)