оглядываться назад на предшествующие детектированные символы. Таким образом преодолевается размножение ошибок.

Посимвольное правило детектирования, описанное выше, не реализует оптимальную схему детектирования для сигналов с парциальным откликом, из-за памяти, свойственной принимаемому сигналу. Все же посимвольное детектирование относительно просто реализуется и оно применяется во многих практических приложениях, использующих дуобинарный и модифицированный сигнальные импульсы. Его качество вычисляется в следующем разделе.

Максимально-правдоподобное последовательное детектирование. Ясно из предыдущего обсуждения, что сигналы с парциальным откликом являются сигналами с памятью. Эту память удобно представить решеткой. Например, на рис. 9.2.11 представлена решетка для дуобинарного сигнала с парциальным откликом для передачи двоичных данных.

Для двоичной модуляции решетка содержит два состояния, соответствующие двум возможным выходным величинам /„,, т.е. /„, =±1. Каждая ветвь в решетке обозначается двумя числами. Первое число слева - это новый символ, т.е. /„,, =±1. Это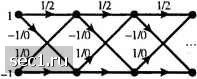

число определяет переход в новое состояние. Число справа - это уровень принимаемого сигнала.

I -1/-2 А -1/-2 I -1/-2 i)k t=D t=T t=2T !=ЗТ

Рис. 9.2.11. Решётка дая дуобинарного сигнала с гюрциальным откликом

Дуобинарный сигнал имеет память длины Z = 1. Следовательно, для двоичной модуляции решетка имеет S,=2 состояния. В общем, для М -ичной модуляции, число

состояний решетки равно Л/.

Оптимальный детектор максимального правдоподобия (МП) последовательности выбирает наиболее правдоподобный путь по решетке после наблюдения последовательности принимаемых данных {Уп,}отсчётных моментах t = mT, /77 = 1,2,... В общем, каждый узел решетки имеет М входящих путей и М соответствующих метрик. Основываясь на величинах метрик, один вход из М приходящих путей выбирается как наиболее вероятный, а остальные М -1 путей и их метрики отбрасываются. Выживший путь в каждом узле затем продолжается в М новых путях, один для каждого из М возможных входных символов, и процесс поиска продолжается. Это в своей основе алгоритм Витерби для выполнения поиска по решетке.

Для класса сигналов с парциальным откликом принимаемая последовательность {>„,, 1</и jV} в общем описывается статически совместной ФПВ /(yll.-.), где

Уы-[У1 Уг ytjf 1 =[1 2--мУ N>L. Если аддитивный шум гауссовский с нулевым средним, f(y\lff) является многомерной гауссовской ФПВ, т.е.

Луы\К)=, . 1,/2 ехр[-КУ;.-КУс -Вл,)], (9.2.60

(2яае1С)

где =[В В2 ... BjY- среднее значение вектора у,, а С является NxN матрицей ковариации для . Затем МП детектор последовательности выбирает последовательность по решетке, которая максимизирует ФПВ /(удг1дг).

Расчёт для нахождения наиболее правдоподобной последовательности по решетке упрощается, если взять натуральный логарифм от /(y;,Iдг). Тогда

\n/(y\K)=-\mni2ndctC)-i(y-BjC-(y-B). (9.2.61) При заданной принимаемой последовательности {у} нахождение последовательности {!„}, которая максимизирует In/(уд,1д,) идентично нахождению последовательности {!„}, которая минимизирует (у, -B,)C"(y, -В,), т.е.

1 = arg min[(y -ВУсСу -В)

(9.2.62)

Вычисление метрик при поиске по решетке усложняется из-за корреляции отсчетов шума на выходе согласованного фильтра для сигнала с парциальным откликом. Для примера, в случае дуобинарного сигнала, корреляция шумовой последовательности {v„}

простирается на два соседних сигнала. Следовательно, v„, и \. коррелированны для

= 1 и некоррелированы для к>1. В общем, сигнал с парциальным откликом с памятью L приводит к коррелированной шумовой последовательности на выходе согласованного фильтра, которая удовлетворяет условию E(y„v„) = О для к> L.B этом случае алгоритм

Витерби для выполнения поиска по решетке может быть модифицирован, как описывается в главе 10.

Некоторое упрощение в вычислении метрик получается, если мы пренебрежем корреляцией шума, предположив, что E(vv) = 0 для к>0. Тогда, при нашем

предположении матрица ковариаций С = а1д,, где al = E(y~), а 1, является NxN единичной матрицей. В этом случае (9.2.62) упрощается

Ij, = arg min

(Уы -ыУ(У1 -B;,)]=arg min

Ы / L

(9.2.63)

где 5„ - Z Jn,-t. = х(Г) - отсчётные значения сигналов с парциальным откликом. В

»-0

этом случае вычисление метрик в каждом узле решетки выполняется так

DM„(/J = DM„, ,(/„ ,)+L-i:V„, .

(9.2.64)

где DM(l)- дистанционные метрики в момент t = mT, DM (\ ) - дистанционные метрики в момент t = {m-\)T, а второе слагаемое в правой части (9.2.64) представляет новое приращение к метрике, основанное на новый принимаемый отсчет у.

Как указано в разделе 5.1.4, МП декодирование последовательности приводит, вообще говоря, к переменной задержке при декодировании каждого кодового информационного символа. На практике, переменная задержки преодолевается путем усечения выживших последовательностей до последних символов, где »SL, так достигается

фиксированная задержка решения. Для случая, когда М выживших последовательностей в момент (-тТ определяют разные значения для символа , то символ может быть

выбран по наиболее вероятной выжившей последовательности. Потери в качестве, связанные с таким усечением, пренебрежимо малы, если N,>5L .

9.2.4. Синтез сигналов для каналов с искажениями

В разделах 9.2.1. и 9.2.2 мы описали правило синтеза сигналов (фильтров) для фильтра

Мы использовали обозначение , чтобы не спутать с 1,.

модулятора на передаче и фильтра демодулятора на приёме для случая идеального канала. В этом разделе мы выполним синтез сигналов при условии, что канал искажает передаваемый сигнал. Мы предполагаем, что частотная характеристика канала С(/)

известна для / <W и что С(/) = О для \f\>W. Правило оптимизации характеристик фильтров G.j-(J) и G{J) обеспечивает максимизацию ОСШ на выходе фильтра демодулятора или, что эквивалентно, на входе детектора. Аддитивный шум канала предполагается гауссовским со спектральной плотностью мощности Ф,.(/). Рис. 9.2.12 иллюстрирует всю рассматриваемую систему.

Фильтр демодлягора

Детектор

Выходные

данные

Гауссовский шум

Рис. 9.2.12. Модель системы для синтеза фильтров модулятора и демодулятора

Сигнальные компоненты на выходе фильтра демодулятора должны удовлетворять условию

Gr(/)C(/)G«(/) = X,(J)e"\ \f\<W, (9.2.65)

где Xj{f) является желательной частотной характеристикой каскада из модулятора, канала и демодулятора, а /д- время задержки, которое необходимо для удовлетворения физической реализуемости фильтров модулятора и демодулятора. Желательную частотную характеристику Xj(f) можно выбрать так, чтобы обеспечить или нулевую МСИ или контролируемую МСИ в точках отсчёта. Мы вьшолним оптимизацию для нулевой МСИ, выбирая Xj(f) = X{f), где А(/)-спектр приподнятого косинуса с произвольным

коэффициентом ската.

Шум на выходе фильтра демодулятора можно выразить так

у(0-Г«(/-т)я(т)Л, (9.2.66)

J 00

где и(0~ входе фильтра. Поскольку «(О" гауссовский процесс с нулевым средним,

то и v(/)-гауссовский процесс с нулевым средним и со спектральной плотностью мощности

Ф™(/) = Ф„„(/)(/)Г- (9.2-67)

Для простоты мы рассмотрим передачу двоичной AM. Тогда выходные отсчёты согласованного фильтра

y.=XoL+v„=L+v„., (9.2.68)

где Хд нормирована к единице, I„=±d, а v„, представляет слагаемое шума, которое является гауссовским с нулевым средним и дисперсией

(9.2 69)

Следовательно, вероятность ошибки равна

Взяв Хд = 1 и 1 =+d имеем в виду, что масштаб х учтён в параметре d. 31-56