dia.

(9.2.70)

Вероятность ошибки минимизируется при максимизации ОСШ = </а или, что эквивалентно, минимизации отношение шум/сигнал csi/d~. Но J- связан со средней

мощностью переданного сигнала так:

(9.2.71)

Gjif) должно быть выбрано так, чтобы удовлетворять условию нулевой МСИ. Следовательно,

М)\ {92.П)

Grif)

и Gt (/) = О для \f\>W. Следовательно,

ndf.

(9.2.73)

d PTi--\C(jf\G,{ff

Таким образом, отношение шум/сигнал, которое должно быть минимизировано по СД/) для /1<Ж,равно

1 flV

1>.(Ж(/)Г#.£-

-.df. (9.2.74)

2 prJ-ПС(/)Г.1а,(/)Г

Оптимальное значение Сд (/) можно найти, использовав неравенство Коши-Шварца

y,(jtdf.iy.Xn\df>\\y,Xn\PAnwJ- (9-2.75) где \L\{f){ и jf/,/)! определены так:

/,(/) = л/Фа7)К(/), \U,i/i = Jf; (9.2.76)

С(/)Ол(/)[

Минимальное значение (9.2.74) получается, если \U, (/)! пропорционально \LL (/) или, что эквивалентно, когда

G,U-)=K

Ф„„(/)"1С(/)

(9.2.77)

где К - произвольная константа. Соответствующий фильтр модулятора имеет амплитудную характеристику

1 К(/)">„„(/)!

.11"

C(/)i

, \f<W.

(9.2 78)

Наконец, максимум ОСШ, достигаемый этими оптимальными на передаче и приёме фильтрами

(9.2.79)

Заметим, что оптимальные фильтры модулятора и демодулятора определены только по амплитудно-частотной характеристике. Фазовые характеристики С.(/) и G,(/) можно выбрать так, чтобы удовлетворить условию (9.2.65), т.е.

©г (/) + ©.(/) +©я (/) = 27i o, (9.2.80)

где 0j-(/), 0<:(/)> Фоью характеристики фильтра модулятора, канала и

фильтра демодулятора, соответственно.

В частном случае, когда аддитивный шум на входе демодулятора гауссовский и белый со спектральной плотностью мощности Лд, оптимальные характеристики фильтров,

определяемые (9.2.77) и (9.2.78), выражаются так

ХЛЛ\

1/2

1/2

f<w.

(9.2.81)

где ЛГ, и ATj- произвольные скалярные множители. Заметим, что в этом случае \G(J) АЧХ фильтра, согласованного с фильтром, имеющим характеристику Gj.(/) .

Соответствующее ОСШ детектора, определяемые (9.2.79), приводится к виду

л-2

d 2РТ

£

(9.2.82)

Пример 9.2.1

Определим оптимальные фильтры на передаче и приёме для двоичной системы связи, которая передает данные со скоростью 4800 бит/с по каналу с частотной характеристикой

С(/)

f<W,

(9.2.83)

где W = 4800 Гц. Аддитивный шум гауссовский, с нулевым средним и спектральной плотностью мощности Ло =10"Вт/Гц.

Поскольку W = \/Т = 4800, мы используем импульс сигнала со спектром приподнятого косинуса с Р = 1. Таким образом,

„:(/) = ini + cos(7tr/)J=rcos

Затем

Gr<J)\ = \GM)

п1/4

9600

9600

/ < 4800

(9.2.84)

(9.2.85)

И800;

и \Gr (f)\ = (/) = 0 в другой области частот. Рис. 9.2.13 даёт АЧХ фильтра Gj. (/) .

Можно теперь использовать эти оптимальные фильтры для определения величины передаваемой энергии g, требуемой для достижения заданной вероятности ошибки. Эта задача оставлена в качестве упражнения для читателя.

-4800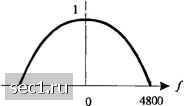

Рис. 9.2.13. Частотная характеристика оптимального фильтра передачи

9.3. ВЕРОЯТНОСТЬ ОШИБКИ ПРИ ДЕТЕКТИРОВАНИИ AM

В этом разделе мы рассчитаем качество демодуляции и детектирования М -ичного сигнала AM в присутствии АБГШ на входе приёмника. Сначала рассмотрим случай, когда фильтры передатчика и приёмника G{f) и Gj.{f) синтезированы для нулевой МСИ. Затем мы рассмотрим случай, когда и Gj.(/) синтезированы так, что

(0 = г(0®л(0 является или дуобинарным или модифицированным дуобинарным двоичным сигналом.

9.3.1. Вероятность ошибки при детектировании AM с нулевой МСИ

В отсутствии МСИ отсчеты принимаемого сигнала на выходе согласованного фильтра приёмника имеют вид

о=1>г(/)# = г;.

(9.3.1)

(9.3.2)

(9.3.3)

а у„,- аддитивный гауссовский шум с нулевым средним и дисперсией

в общем принимает одно из М возможных равно удаленных значений амплитуды

с равной вероятностью. При заданном частном значении уровня амплитуды задача сводится к определению вероятности ошибки.

Задача расчета вероятности ошибки для цифровой AM в ограниченном по полосе канале с АБГШ в отсутствии МСИ идентична расчету вероятности ошибки М -ичных AM, данному в разделе 5.2. Окончательный результат, который был получен, таков

(9.3.4)

Но %g =3fS/(M - I), а % =fKp~ средняя энергия на символ, а средняя энергия

на бит.

Следовательно

2(М-1)

6(log,M)

(9.3.5)

Это в точности форма для вероятности ошибки в Л/-ичной AM, полученная в разделе 5.2 (смотри (5.2.46)). В трактовке AM настоящей главы мы навязываем дополнительное условие, что передаваемый сигнал ограничен полосой, пропускаемой каналом. Следовательно, передаваемые импульсы сигнала синтезированы как ограниченные по полосе и приводящие к нулевой МСИ.

В противоположность этому, ограничение по полосе не было навязано сигналам AM, рассмотренным в разделе 5.2. Тем не менее, приёмники (демодуляторы и детекторы) в обоих случаях оптимальны (согласованные фильтры) для соответствующих переданных сигналов. Следовательно, нет потерь в качестве (вероятности ошибки), обусловленных ограничением полосы, если импульс сигнала синтезирован для нулевой МСИ, а канал не искажает передаваемый сигнал.