Таблица 9.4.3. Кодовая таблица для кода переменной длины (2,7). Входные символы данных Кодированные выходные последовательности

х=0, если предыдущий входной символ 1, х=1, если предыдущий входной символ 0.

Если входной информационный символ 1, то выход кодера 01. Декодирование этого кода простое. Первый символ двухсимвольного блока избыточный и может быть отброшен. Второй символ - это информационный символ. Этот код обычно называется кодом Миллера. Видим, что это код с зависимыми состояниями, которые описываются диаграммой состояний, показанный на рисунке 9.4.5. Имеются два состояния, обозначаемые Л, и Л,. с переходами, указанными на рисунке. Когда кодер в состоянии .V, то входной символ 1 приводит к тому, что кодер остается в состоянии .V, а выход кодера 01 Это обозначено 1/01. Если входной символ О, кодер переходит в состояние S.,. а выход кодера 00. Это обозначено 0/00. Аналогично, если кодер в состоянии то входной символ О не вызывает переход, а выход кодера 10. С другой стороны, если входной символ 1, кодер переходит в состояние .S,, а выход кодера 01. Рис. 9.4.6 показывает решётку для кода Миллера.

1/01 0/10

1/01

Рис. 9.4.5. Диаграмма состояний для кода Миллера (d=l, к=3)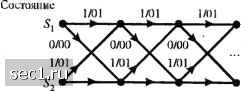

0/10

0/10

0/10

Рис. 9.4.6. Решётка для кода

Миллера (rf=l, к-3)

Отображение кодовых символов в сигналы. Выходная последовательность (с1,к) кодера отображается модулятором в сигнал для передачи по каналу. Если двоичный символ 1 отображается прямоугольным импульсом амплитуды А, а двоичный символ О отображается прямоугольным импульсом с амплитудой -А результатом является {с/,к) кодированный сигнал ДБН (NRZ). Заметим, что длительность прямоугольных кодовых импульсов равна = Я/Яь - Кь тае Rf, - информационная скорость на входе кодера, Т-битовый интервал (не кодированных символов), а R - скорость кода для {с1, к) кода

Когда (d,K) код с фиксированной длинной и независимыми состояниями имеет скорость R. =к/п, мы можем рассматривать образование каждого и-символьного блока, как генерирование одного сигнала длительностью пТ. Таким образом мы имеем М-!*

сигналов, один для каждого из 2* возможных п символьных блоков. Эти кодированные сигналы имеют общую форму, определённую (4.3.6) и (4.3.38). В этом случае нет зависимости между передаваемыми последовательными сигналами.

В противоположность ситуации, рассмотренной выще, модулированный сигнал имеет память, если используют сигнал ДБНП и (или) код (с/,к) имеет зависимые состояния. Рассмотрим влияние отображения кодовых символов в ДБНП сигнал.

Напомни, что зависимость состояний ДБНП сигнала обусловлена дифференциальным кодированием информационной последовательности. Дифференциальное кодирование является формой предварительного кодирования, которое описывается математически так

где {d} является двоичной последовательностью на входе предварительного кодера

предкодера, {/}-выходная последовательность символов предкодера, а Ш означает

суммирование по mod 2. Это кодирование характеризуется диаграммой состояний, показанной на рис. 9.4.7(a).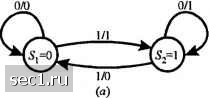

0Ы1)

OlsU)

о/о О/О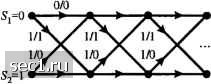

0/1 0/1

Рис. 9.4.7. Диаграмма состояний и решётка состояний для сигнала ДБНП (NRZI)

Последовательность {р) передаётся посредством сигнала ДБН. Таким образом, когда Pi=\, то выход модулятора является прямоугольным импульсом амплитуды А, а когда р=0 - выходом модулятора является прямоугольный импульс амплитуды ~А. Когда кодирование отображается диаграммой состояний рис. 9.4.7(a) мы получаем соответствующую диаграмму состояний, показанную на рис. 9.4.7(b). Соответствующая решётка показана на рис. 9.4.7(c).

Когда выход кодера (d, к) с зависимыми состояниями подаётся на ДБНП модулятор, мы можем просто сочетать две диаграммы состояний в единую диаграмму состояний для {d, к) кода с предварительным кодированием. Аналогичное сочетание можно выполнить с соответствующими решётками. Следующий пример иллюстрирует подход для кода Миллера (1, 3) обслуживающий ДБНП модулятор.

Пример 9.4.7. Определим диаграмму состояний комбинации кода Миллера (1, 3), за которым следует предварительное кодирование, свойственное ДБНП модуляции. Поскольку код Миллера (1, 3) имеет два состояния и предкодер имеет два состояния, диаграмма состояний комбинированного кодера имеет четыре состояния, которые мы обозначим так 5д,) = (а,,5,), (a,,), (а,-,), (а-,,-,), где S={ai,cy} представляют

два состояния кода Миллера, а -{1,2} представляют два состояния предкодера для ДБНП. Для каждого символа входных данных кодера Миллера мы получаем два выходных символа, которые затем идут на предкодер, превращаясь в два выходных символа предкодера. Результирующая диаграмма состояний показана на рис. 9.4.8, где первый символ означает информационный символ на входе кодера Миллера, а следующие два символа представляют соответствующий выход предкодера. Решётчатую диаграмму состояний для подвергающейся предварительному кодированию последовательности Миллера можно получить непосредственно из комбинированной диаграммы состояний или из комбинаций решёток двух кодов. Результатом такого комбинирования является решетка с четырьмя состояниями, одна ступень которой показана на рис. 9.4.9.

Читатель в порядке упражнения может попытаться показать, что четыре сигнала, полученные отображением каждой пары символов предварительно кодированной последовательности Миллера в ДБН сигнал, биортогональны и что результирующий модулированный сигнал идентичен сигналу, полученному модуляцией с задержкой, описанной в разделе 4.3.2.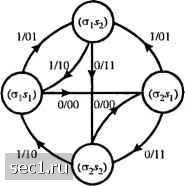

Рис. 9.4.8. Диаграмма состояний каскадного соединения кода Миллера и ДБНП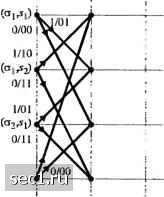

1/10

(£12,2)

Рис. 9.4.9. Один шаг решй1чатой диаграммы каскадиоп) соединения кода Миллера и ДБНП

Из диаграмм состояний с зависимыми состояниями можно получить матрицу вероятностей переходов, как описано в разделе 4.3.2. Затем можно определить спектральную плотность мощности кодированных сигналов, как показано в разделе 4.4.3.

9.5. БИБЛИОГРАФИЧЕСКИЕ ЗАМЕЧАНИЯ И ССЫЛКИ

Основополагающая работа по синтезу сигналов для ограниченных по полосе каналов выполнена Найквистом (1928). Использование двоичных сигналов с парциальным откликом было первоначально предложено Лендером (1963) и было позднее обобщено Кретчмером (1966). Другие ранние работы по проблемам, имеющим отношение к межсимвольной интерференции (МСИ) и оптимизации передатчика и приёмника для ограничений МСИ даны Герстом и Даймондом (1961), Тафтсом (1965) Смитом (1965) и Бергером и Тафтсом (1967). Передача «быстрее Найквиста» изучалась Мазо (1975) и Фошини(1984).