х(иГ) =

парциальный отклик при « = О равен нулю по модзлю /\/ . Например, рассмотрите желательный отклик для Л/ = 2:

2 (и = 0).

1 (" = !)

-1 (« = 2), О (для других п).

Покажите, почелгу такой отклик нельзя подвергнуть предварительному кодированию. 9.22. Рассмотрите RC фильтр низких частот, показанный на рис. Р9.22, где т = RC = 10" .

Вход

Выход

Рис. Р9.22

a) Определите и нарисуйте задержку огибающей (групповую задержку) фильтра, как функцию от частоты.

b) Предположите, что вход фильтра - низкочастотный сигнал с полосой 4/" = 1 кГц. Определите отклик RC фильтра на этот сигнал

9.23. Микроволновый радиоканал имеет частотную характеристику

C(/)-l+0,3cos27t/r.

Определите частотные характеристики оптимального перелающего и приёмного фильтров, которые дают нулевое МСИ при скорости \/Т символов/с при наличии 50 % избыточной полосы. Предположите, гго спектр аддитивного шума равномерный.

9.24. Четырёхпозиционная AM используется для передачи с битовой скоростью 9600 бит/с по каналу, имеющему частотную характеристику

С(Л =--

1 + 7( 2400)

для I/ <2400 и С(/)-0 вне этой области частот. Аддитивный шум яв.аяется гауссовским, белым с нулевым средним и спектральной плотностью лющности i-M Вт/Гц. Определите (.шплитудныс) частотные

хар;1ктеристик11 оптимального фильтра на передаче и прис.ме.

9.25. Определите пропускную способность кода (0,1) с ограниченным разбегом. Сравните эт> пропускную способность с той же характеристикой для кода (I, оо) и объясните соотношения.

9.26. Троичный фор.мат сигнала синтезируется для канала, который не пропускает постоянною составляющую. Входная двоичная информационная последовательность передастся путём отображения 1 или в положительный, или отрицательный импульс, а О передается отсутствием и.мпульса. Следовательно, для персдг1чи 1 полярность импульса чередуется. Это называют AMI (alternate mark inversion) кодом. Определите пропускную способность кода.

9.27. Дайте др.угое описание AMI кода, описанного в задаче 9.26, используя набегающую сумму цифр (RDS) с ограничением, что RDS может принимать только значения О и +1.

9.28. (Коды АВпТ, В - binary, Т - ternary). В задаче 9.26 обрапгге внимание, что AMI является «псевдотроичным» кодом, в котором для передачи одного бита информации используется троичный символ, имеющий информационнуто ё.\1кость logj 3 = 1,58 бит. Этот код не обеспечивает необходимую форму спектра Лучшую форму спектра даёт код, обозначаемый как кВпТ, где к означает количество информационных бит, an- число трои»шых символов на блок. При выборе наибольшего возлюжного к для каждого п получается следующая таблица:

Определите эффективность этих кодов путём вычисления отношения k/{nlog22). Заметьте, что 1В1Т -это код AMI.

9.29. Эта задача имеет де.то с пропускной способностью двух (d, к) кодов.

а) Определите пропускную способность (d,K) кода, который имеет следующую матрицу переходов состояний

1 1

Ь) Повторите (а) для

1 О

I 1

О 1

с) Прокомментируйте разницу (а) и (Ь).

9.30. Простейшая модель телеграфного кода состоит из двух символов (Блэихут, 1990). Точка содержит элемент сигнала «1» и «О». Тире состоит из трёх следующих без перерыва элементов «1» и одного элемента «0>>. >

. Рассмотрите этот код как код, составленный из символов равной длительности. Определите матрицу переходов состояний. Определите информационную ёмкость кода.

9.31. Определите матрицу переходов состояний кода с ограниченным разбегом, который описывается диафаммой состояний, показанной на рис. Р9.31. Нарисуйте соответствующую решетку.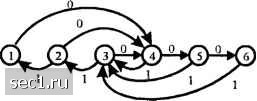

Рис. Р9.31

9.32. Определите матрицу переходов состояний для кода (2,7) с офаниченным разбегом, удовлетворяющего диаграмме состояний, показанной на рис. Р9.32.

- О - О -0 - О - О 0 0

W 1 , г 1 , г 1 , г ] W 1 W 1

Рид. Р9.32

связь в ОГРАНИЧЕННЫХ ПО ПОЛОСЕ ЛИНЕЙНЫХ ФИЛЬТРОВЫХ КАНАЛАХ

в гл. 9 мы сосредоточили внимание на синтезе фильтров модулятора и демодулятора для ограниченных по полосе каналов. Процедура синтеза основывалась на предположении, что частотная характеристика (идеального или неидеального) канала С(/) известна априори. Однако в практике цифровых систем связи, рассчитанных на высокоскоростную передачу через ограниченные по полосе каналам, частотная характеристика С(/) не известна с достаточной точностью для возможности синтеза оптимальных фильтров модулятора и демодулятора. Например, при цифровой связи по коммутируемым телефонным сетям канал связи различен каждый раз при наборе нового номера, поскольку маршрут по каналу каждый раз различен. Это пример канала, характеристики которого не известны априори. Имеются другие типы каналов, например беспроводные, такие как радиоканалы и подводные акустические каналы, чьи частотные характеристики переменны во времени. Для таких каналов нет возможности синтезировать оптимальные фиксированные фильтры для демодулятора.

В этой главе мы рассмотрим проблему синтеза приёмника в условиях искажений в канале, не известных априори, и наличия АБГШ. Искажения в канале приводят к МСИ, которая, оставаясь некомпенсированной, часто вызывает ошибки. Решение проблемы МСИ можно свести к синтезу приёмника, который использует способ компенсации или сокращения МСИ в принимаемом сигнале. Компенсатор МСИ назван эквалайзером или выравнивателем.

Здесь рассматриваются три вида методов выравнивания. Один из них основывается на правиле максимально-правдоподобного (МП) детектирования последовательностей, и является оптимальным с точки зрения вероятности ошибки. Второй метод выравнивания основывается на использовании линейного фильтра с регулируемыми коэффициентами. Третий метод выравнивания, который использует символы, продетектированные раньше, для подавления МСИ при детектировании текущего символа назван выравниванием с обратной связью по решению. Мы начнём с рассмотрения оптимального детектора для каналов с МСИ.

10.1. оптимальный приемник для канала с мси и абгш

В этом разделе мы рассмотрим структуру оптимального демодулятора и детектора для цифровой передачи по неидеальному, ограниченному по полосе, каналу с аддитивным гауссовским шумом. Мы начнем с передаваемого (эквивалентного низкочастотного) сигнала, определяемого (9.2.1). Принимаемый сигнал (эквивалентный низкочастотный) выражается так

r,(/) = Z iM-»T)+<t), (10.1.1)

где h{t) представляет отклик эквивалентного низкочастотного канала на входной сигнальный импульс gif), а z{t) представляет АБГШ.