Сначала мы покажем, что оптимальный демодулятор можно реализовать как фильтр, согласованный с h{t), за ним идет операция стробирования со скоростью передачи символов 1/7 и последующий алгоритм обработки для оценивания информационной последовательности {/„} по принятым отсчётным значениям. Следовательно, отсчеты на выходе согласованного фильтра достаточны для оценивания последовательности {/„}.

10.1.1. Оптимальный приёмник максимального правдоподобия

Представим принимаемый сигнал r,(f) в виде разложения

/;(/) = lim ;г,Л(0,

(10.1.2)

где {ftO)}" полная система ортонормированных функций, а {/;}- наблюдаемые (на фоне шума) случайные величины, полученные проектированием /)(/) на ансамбль (/.(О}-Легко показать, что

(10.1.3)

где величина, полученная от проектирования h{i~nT) на /(J), а z-величина,

полученная от проектирования z{f.) на /(0- Последовательность {z] является гауссовской с нулевым средним и ковариацией

(10.1.4)

Совместная ФПВ случайных величин Гд, = [,2 ••л,] при условии передачи последовательности 1, s[/, Д ...7], где p<N, равна

Г Y f м

(10.1.5)

в пределе, когда число N наблюдаемых случайных величин становится неограниченным, логарифм pifj 1р) пропорционален метрикам РМ(\р), определяемые так

РМ(1 ) = -

r,(/)rf/ + 2Re2:

r,{t)h\t-nT)dt

(10.1.6)

-YLO.]h\t nt)h(t-mT)dt.

n Ш -CO

Максимально-правдоподобные оценки символов /,, Д,...,/,-это такие, которые

максимизируют (10.1.6). Заметим, однако, что интеграл от а}(/) общий для всех метрик и, следовательно, его можно исключить. Второй интеграл, включающий r,(t), зависит от

величины

y„y{nr)-\rXt)h\t rrr)dt. (10.1.7)

-□о

Эти величины можно генерировать, пропуская r,(l) через фильтр, согласованный с

h(t) и стробируя выход со скоростью 1/Г. Отсчеты образуют ряд достаточных

статистик для вычисления РМ(1р) или, что эквивалентно, корреляционных метрик

CM(IJ = 2Re

где, по определению, x(i) - отклик согласованного фильтра на h(i), а

х„ в х(/Г) = \h\i)h(t + nT)dt.

(10.1.9)

Таким образом, x{t) представляет выход фильтра, имеющего импульсную характеристику hirt) и вход Л(/). Другими словами, x{f) представляет автокорреляционную функцию h{t). Соответственно {х) представляют отсчёты автокорреляционной функции Л(/), взятые периодически через 1/Г. Мы не интересуемся тонкостями построения фильтра, согласованного с /;(/), поскольку на практике мы можем ввести необходимую задержку, чтобы обеспечить реализуемость согласованного фильтра.

Если мы подставим для /•,(/) в (10.1.2) соотношение (10.1.1) мы получим

A=ZA-„ + v., (10.1.10)

где Vj. означает последовательность отсчётов аддитивного шума на выходе фильтра, т.е.

\f, = \z{t)h\t-kT)dt. (10.1.11)

Выходы демодулятора (согласованного фильтра) в моменты отсчёта искажены МСИ, как указано в (10.1.10). В любой практической системе разумно предположить, что МСИ влияет на ограниченное число символов. Таким образом, мы можем предположить, что х„ = о для и > L. Следовательно, МСИ, наблюдаемую на выходе демодулятора, можно

рассматривать как выход машины с конечным числом состояний. Это позволяет выход канала с МСИ представить диаграммой решётки, а оценки максимального правдоподобия информационной последовательности (/,,/2,...,/) определяются наиболее вероятным

путём по решётке, при данной принятой на выходе демодулятора последовательности {у„}. Ясно, что алгоритм Витерби обеспечивает эффективный метод выполнения поиска по такой решётке.

Метрики, которые вычисляются при максимально правдоподобном последовательном оценивании (МППО, MLSE) последовательности [1}, определены (10.1.8). Можно

видеть, что эти метрики можно вычислить рекуррентно посредствам алгоритма Витерби согласно соотношению

/ L \

CM„(IJ = CM„ .(I„ ,) + Re

2y„-xJ„-2j;xJ„ „

(10.1.12)

На рис. 10.1.1 дана блок-схема оптимального приёмника для канала с МСИ и АБГШ.

I время f кТ

Рис.10.1.1. Оптимальный приёмник для канала с АБГШ и МСИ

10.1.2. Модель канала с МСИ с дискретным временем

При рассмотрении ограниченных по полосе каналов с МСИ удобно разработать эквивалентную модель с дискретным временем для аналоговой (с непрерывным временем) системы. Поскольку передатчик посылает символы в дискретные моменты времени со скоростью 1/7" символов в секунду, а стробированный выход согласованного фильтра приемника также является сигналом дискретного времени с отчетами, возникающими со скоростью l/r, то следует, что каскадное соединение аналогового фильтра передатчика с импульсной характеристикой g{/), канала с импульсной характеристикой с(/), согласованного фильтра в приемнике с импульсной характеристикой h*{-l) и стробирующего устройства можно представить эквивалентным трансверсальным фильтром с дискретным временем, имеющий набор коэффициентов усиления (х.}.

Следовательно, мы имеем эквивалентный трансверсальный фильтр с дискретным временем, который покрывает временной интервал 1LT секунд. Его входом является информационная последовательность символов {1к}у выходом является последовательность с дискретным временем {у}, определяемая (10.1.10). Эквивалентная модель с дискретным временем дана на рис. 10.1.2.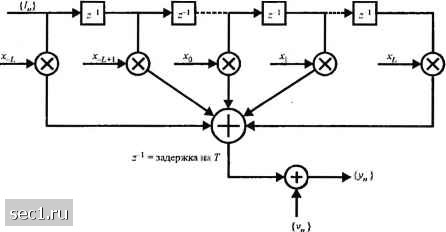

Рис. 10.1.2. Эквивалентная модель дискретного времени для канала с МСИ

Основная трудность при использовании этой. модели с дискретным временем возникает при оценивании качества различной техники выравнивания или техники оценивания, что обсуждается в следующих разделах. Трудности обусловлены корреляцией отсчётов шумовой последовательности {vj на выходе согласованного фильтра. Ряд

шумовых величин {v} образуют последовательность с гауссовским распределением, с нулевым средним и автокорреляционной функцией (смотри задачу 10.5)

£(v;v)=

NqX, {к j<L) [ О (при других к, j)

(10.1.13)

Таким образом, шумовая последовательность коррелирована, если не выполняется условие = О, к:0. Поскольку более удобно иметь дело при расчёте такой

характеристики качества как вероятность ошибки с белой шумовой последовательностью, то желательно обелить шумовую последовательность путём дальнейшей фильтрации последовательности [у,].