Обеляющий фильтр с дискретным временем определяется следующим образом: Пусть X{z) обозначает (двухстороннее) z-преобразование отсчетов автокорреляционной функции {х},т.е.

X(z)=fx,z-. (10.1.14)

k=-L

Поскольку х. -х , следует X(z) = X(z ) и 2L корней X(z) имеют симметрию, так

что, если р корень, то 1/р* тоже корень. Следовательно, X{z) можно факторизовать и выразить так

X(z) = F(z)F(z-), (10.1.15)

где F{z)- полином степени/., имеющий корни р,, р,p, а F*(z )- полином степени /,, имеющий корни 1/р*, l/p,, 1/pI- Подходящий обеляющий фильтр имеет г-преоб-разование МF(z ). Поскольку имеется 2 возможных способов выбора корней F(z"), а каждый выбор ведет к фильтру, который одинаков по амплитудной характеристике и различен по фазе по сравнению с другими выборами, то мы предлагаем выбрать уникальное F\z~), имеющее минимальную фазу, т.е. полином, имеющий все свои корни внутри единичного круга. Тогда все корни F*(r") лежат внутри единичной окружности (с центром в начале координат), а 1/F*(z")- физически реализуемый, устойчивый фильтр с дискретным временем. Следовательно, пропуская последовательность {у) через цифровой фильтр \IF{z~) получаем выходную последовательность (и), которую .можно представить так

л-=Е/Л-„+Л*, (10.1.16)

где (Л;.)- последовательность отсчетов гауссовского белого шума с нулевым средним, а l/j)- набор взвешивающих коэффициентов в эквивалентном трансверсальном фильтре с дискретным временем, имеющий передаточную функцию F{z) (причём не F{z )). В общем последовательность {и.} комплексная .

В совокупности каскадное соединение фильтра передатчика g{l\ канала согласованного фильтра h*(-t), стробирующего устройства и фильтра для взвешивания шума с дискретным временем \IF*{z ) можно представить в виде эквивалентного трансверсального фильтра с дискретным временем, имеющего набор взвешивающих коэффициентов {/,.}. Аддитивная шумовая последовательность (т]*}. искажающая сигнал на выходе трансверсального фильтра с дискретным временем, является белой гауссовской шумовой последовательностью с нулевым средним и дисперсией N. Рис.10.1.3

иллюстрирует модель эквивалентной дискретной системы с белым шумом.

Мы будем ссылаться на эту модель, как на эквивалентную модель с дискретным временем и белым шумом.

Пример 10.1.1. Допустим, что сигнальный импульс передатчика g{t) имеет длительность Г и единичную энергию, а принимаемый сигнальный импульс равен h{t) = git)+ag{(-r).

Определим эквивалентную модель с дискретным временем и белым шумом. Отсчеты автокорреляционной функции определены так

a ik = ~\) l + (k-Q) a {k = 1).

(10.1.17)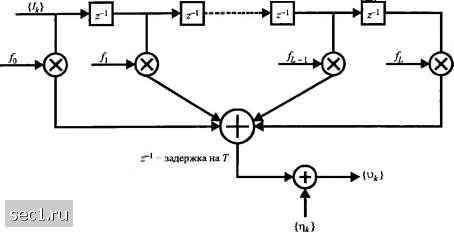

Рис. 10.1.3. Эквивалентная модель дискретного времени для канала с МСИ и АБГШ

Затем, z-преобразование даёт

X(z)= xz"* =a*z + (l + a) + az- =(az +l)(a*z + l).

(10.1.18)

*= 1

Предполагая, что

>1, выберем F(z) = az+1 так, чтобы эквивалентный

трансверсальный фильтр состоял из двух ячеек, имеющих коэффициенты усиления ячеек f=\f=a. Заметим, что корреляционную последовательность (х} можно выразить

через {/„} так

к = 0,1, 2,...,L.

(10.1.19)

Если канальный отклик меняется медленно со временем, согласованный фильтр приемника становится меняющимся во времени фильтром (с переменными параметрами). В этом случае изменение во времени пары канал - согласованный фильтр приводит к фильтру с дискретным временем с переменными во времени коэффициентами. Как следствие, мы имеем эффект переменной во времени МСИ, которую можно моделировать фильтром, показанным на рис. 10.1.3, у которого коэффициенты медленно меняются во времени.

Линейная фильтровая модель с дискретным временем и белым шумом для МСИ отражает то, что происходит при высокоскоростной передаче по идеальному ограниченному по полосе каналу. Она будет использоваться на протяжении всей этой главы при обсуждении техники компенсации МСИ. В общем, методы компенсации называют техникой выравнивания или алгоритмом выравнивания

10.1.3. Алгоритм Витерби для модели фильтра с дискретным временем и белым шумом

Алгоритм Ml 1110 для оценки информационной последовательности {7,} "наиболее легко описывается через принимаемую последовательность (и.) на выходе обеляющего фильтра. В присутствии МСИ, которое покрывает L+\ символа (L интерферирующих

компонент), реализация правила МППО эквивалентно оцениванию состояния конечного автомата с дискретным временем. Конечный автомат в этом случае является эквивалентом канала с дискретным временем с коэффициентами {/}, а его состояние в любой момент

времени определяется L новыми (последними) входами, т.е. состояние в точке к определяется так:

.=(Л-,>Л-2,-,4 J, (10.1.20)

где - О для А: < О. Таким образом если информационные символы являются М -

ичными, канальный фильтр имеет М состояний. Следовательно, канал описывается состояниями решётки и алгоритм Витерби можно использовать для определения наиболее вероятного пути на решетке.

Метрики, используемые в поиске по решётке, подобны метрикам, используемым при декодировании мягких решений свёрточных кодов. Вкратце, мы начинаем с отсчётов и,, и,, ...,u,, по которым вычисляем М* метрик

(10.1.21)

М* возможных последовательностей 4.,, 4, ..../j,/j подразделяется на М групп, соответствующих состояниям 4,, 4, ..-../j. Заметим, что М последовательностей в каждой группе (состояний) отличается в символе /j и соответствуют путям по решетке.

которые сходятся в одном узле. Из М последовательностей в каждом из М состояний мы выберем последовательность с наибольшей вероятностью (по отношению к /,) и определяем для выживших последовательностей метрики

PM,(I,.,) = PM,(/,,„/„...,4) = max]ln/)(vJ/„/, „...,/, J. (10.1.22)

M-L оставшихся последовательностей из каждой из М групп исключаются. Таким образом мы оставляем выживших последовательностей и их метрик.

При приеме u2 М выживших последовательностей расширяются на один шаг и

вычисляются соответствующие М* вероятностей для расширенных последовательностей, используя предыдущие метрики и новое приращение, которое равно ln?(o242>4+l.•••4)• Снова М последовательностей делятся на М групп, соответствующих М возможным состояниям (42. "-.A) каждой группы выбирается наиболее вероятная последовательность, в то время как другие М-\ последовательностей отбрасываются.

Описанная процедура продолжается с приемом последовательных сигнальных отсчетов. В общем при приёме u ;t вычисляются метрики

Л.(1...) = тах[1пр(у,,,/,,„...,/,) + РМ, ,(1,,,.,)] (10.1.23)

и определяются вероятности М выживших последовательностей. Таким образом по мере приема каждого отсчета сигнала, алгоритм Витерби включает В себя сначала вычисление

Л</* вероятностей

(10.1.24)

Мы видели, что метрики РМк{Г) связаны с евклидовым расстоянием DMk(J), когда аддитивный шлм гауссовский.