соответствующих Л/* последовательностям, которые формируют продолжение выживших последовательностей на предыдущих шагах процесса. Затем М* последовательностей подразделяются на групп. Каждая группа содержит М

последовательностей, которые заканчиваются тем же набором символом ..t,и

отличается в символе Д. Из каждой группы из К4 последовательностей мы выбираем одну, имеющую наибольшую вероятность, как отмечено (10.2.23), в то время как оставшиеся М-1 последовательностей исключаются. Таким образом мы оставляем снова М последовательностей, имеющие метрики PM(lj).

Как отмечено ранее, задержка в детектировании каждого информационного символа по Витерби, вообще говоря, меняется. На практике изменение задержки устраняют путём удержания выживших последовательностей с q последними символами, где q»L. Тем

самым достигается фиксированная задержка. В случае, когда М выживших последовательностей на к -м шаге не совпадают в символе , можно выбрать символ в

наиболее вероятной последовательности Потеря в качестве, возникающая из-за этой субоптимальной процедуры оценивания, пренебрежимо мала, если q>5L.

Пример 10.1.2. Для иллюстративных целей предположим, что для передачи четырехуровневой (М=4) AM используется дуобинарный сигнальный импульс. Таким образом, каждый символ - это число, выбираемое из ряда (-3, -1, 1, 3). Контролируемая МСИ в этом сигнале с парциальным откликом представлена эквивалентной моделью канала с дискретным временем, показанной на рис. 10.1.4. Предположим, мы приняли отсчеты U, и Uj, где

и, =/, +Г1,

(10.1.25)

Вход Д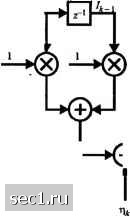

Выход

Рис. 10.1.4. Эквивалентная модель дискретного времени для межсимвольной интерференции, образованной дуобинарным импульсом

а {л,} является последовательностью статистически независимых гауссовских случайных величин с нулевым средним. Мы можем теперь вычислить 16 метрик

к=\ \ j=o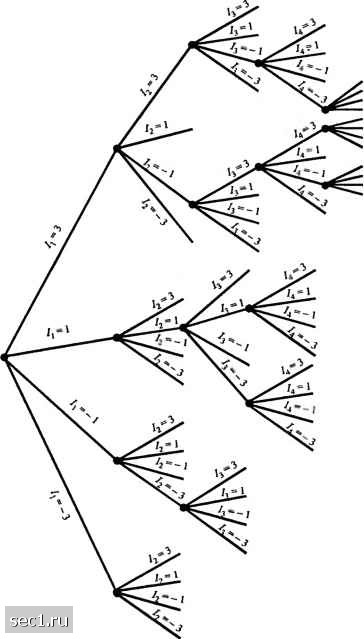

t t t

где 4=0 для k<Q.

Заметим, что не все последовательно принимаемые сигналы {о,} включают в себя /,.

Таким образом, на этом шаге мы можем исключить 12 из 16 возможных пар {/,,/2}- Этот шаг иллюстрирует древовидная

диаграмма, показанная на рис. 10.1.5.

Другими словами, после вычисления 16 метрик, соответствующих 16 путям древовидной диаграммы, мы исключаем три из четырех возможных путей, которые кончаются на 2=3 и накапливаем наиболее

правдоподобные из этих четырёх. Таким образом, метрики для выживших путей равны 1 г

РМ,(,1=Х /,) = тах

-Z -.-Ел.

Рис. 10.1.5. Древовидная диафамма для декодирования по Витерби дуобинарного импульса

Процесс повторяется для каждого набора четырех путей, заканчивающихся на 2 4 = -1 и /, = -3. Таким образом, четыре пути и их соответствующие метрики

выживают после того, как приняты U, и Uj.

Когда принято Uj, четверо

путей расширяется так, как показано на рис. 10.1.5, чтобы производить 16 путей и 16 соответствующих метрик,

определяемых так

рм,(/з,4,/,) = Рм.(/2,/,)-

(10.1.27)

Из четырех путей, заканчивающихся 1з-3 мы сохраняем наиболее правдоподобные. Это процедура снова повторяется для 4=1, 4=~1 4=~3. Следовательно, только четверо путей выживают на этом шаге. Процедура затем повторяется для каждого последовательного принимаемого сигнала и для к>3.

10.1.4. Качество алгоритма МППО для каналов с МСИ

Теперь определим вероетность ошибки при использовании алгоритма МППО (MLSE) для принимаемой информационной последовательности, если информация предается посредством AM, а аддитивный шум в канале гауссовский. Похожесть между свёрточным кодом и МСИ конечной длительности в канале подразумевает, что метод вь1числения вероятности ошибки последней вытекает из первой. В частности, метод вычисления качества декодирования мягких решений сверточного кода посредствам алгоритма Витерби, описанный в разделе 8.2.3, применим здесь с некоторой модификацией.

При использовании в канале с аддитивным гауссовским шумом и МСИ сигналов AM, метрики, используемые в алгоритме Витерби, можно выразить как в (10-1-23) или, что эквивалентно, так

г , №

(10.1.28)

где символы {/„} могут принять значение ±d, ±3d, ..., + {М-\)d, а 2d- это расстояние

между соседними уровнями. Решетка имеет состояний и определяется в момент к так

S,(I,„ .,!, ,). (10.1.29)

Обозначим оцененные символы посредством алгоритма Витерби через (/„}, а соответствующие оцененные состояние в момент к так

s,=(7,J,„...X j. (10.1.30)

Теперь предположим, что оцениваемый путь по решётке ответвляется от правильного пути в момент к и сливается с правильным путём в момент к+\. Таким образом, S. = и

-k+i Д-я к <т <к + L. Как и в свёрточном коде, мы назовём это

ошибочным событием. Поскольку МСИ канала простирается на L + \ символов, то следует, что / > L +1

Для такого ошибочного события мы имеем и /. i, но /„, = 1 для

k-L<m<k-\ и k+l-L<m<k+l-\. Удобно определить вектор ошибки е, соответствующий этим ошибочным событием, так

£ = 8,, ... 8,,, , ,], (10.1.31)

где компоненты s определяются так

еу-(Л-/,), j = k, к + \..., k+I-L-\. (10.1.32)

Нормирующий множитель \/2d в (10.1.32) приводит к тому, что элемент принимает значения ±1, ±2, ±3,±(Л/-1). Более того, вектор ошибок характеризуется свойствами, что £ О, е., i j 0 и что нет последовательности из L соседних элементов, которые равны нулю. С вектором ошибок в (10.1.31) связан полином степени I-L- \.

е(2) = + 8,,,z- + 8,,,z- +... + 6,,, , .z с--). (10.1.33)

Мы хотим определить вероятность появления ошибочного события, которое начинается в момент к и характеризуется вектором ошибок s, определяемым (10.1.31) или, что эквивалентно, полиномом (10.1.33). Чтобы найти его, будем следовать процедуре, разработанной Форни (1972). Конкретнее, чтобы произошло ошибочное событие s, должны произойти следующие три подсобытия £,, и Е:

£,: в момент к, S.=S;