символа для формирования решения 1. Если 4 не идентично передаваемому символу 1 имеет место ошибка.

1 locKupp кТ>р«ван1Я.1Й

вход

Скоррй1сгирова1111ый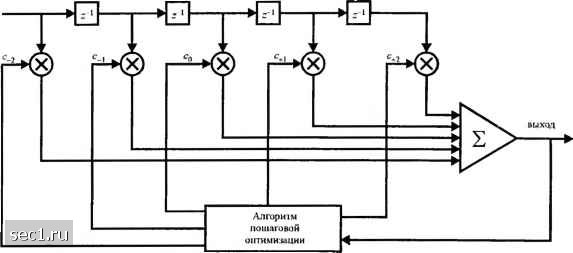

Рис. 10.2.1. Линейный трансвсрсальный фильтр

Значительные исследования были выполнены по нахождению критерия оптимизации коэффициентов фильтра [с}. Поскольку наиболее употребительная мера качества для

цифровой системы связи - это средняя вероятность ошибки, желательно выбрать коэффициенты так, чтобы минимизировать этот показатель качества. Однако вероятность ошибки существенно нелинейная функция {с}. Следовательно, вероятность ошибки как

показатель качества для оптимизации взвешивающих коэффициентов ячеек эквалайзера не практичен.

Два критерия нашли широкое распространение при оптимизации коэффициентов {с}

эквалайзера. Один-это критерий пикового искажения, а второй - критерий среднеквадратичной ошибки.

10.2.1. Критерий пикового искажения

Пиковое искажение просто определяется как наиболее плохой случай МСИ на выходе эквалайзера Минимизацию этого показателя качества называют критерием пикоього искажения. Сначала мы рассмотрим минимизацию пикового искажения, предполагая, что эквалайзер имеет неограниченное число ячеек. Затем мы обсудим случай, когда трансверсальный эквалайзер имеет конечное число ячеек.

Мы видели, что каскадное объединение модели линейного фильтра дискретного времени с импульсной характеристикой {/„} и эквалайзера, имеющего импульсную характеристику {с„}, можно представить одним эквивалентным фильтром с импульсной характеристикой

(10.2.2)

Это значит, что {Цп) - это просто свертка {с„} и (/„}. Считается, что эквалайзер имеет неограниченное число ячеек. Его выход в к-й отсчетный момент можно выразить в виде

к = 4oh + Е.Л.-; • (10.2.3)

Первое слагаемое в (10.2.3) представляет взвешенная версия желательного символа. Для удобства, мы нормируем qo к единице. Второе слагаемое является МСИ. Пиковое значение этой интерференции, которое называется пиковым искажением, равно

Я=-00

п=-<о л* о

у-а.

(10.2.4)

Таким образом, 2)(с) является функцией взвешивающих коэффициентов ячеек эквалайзера.

При помощи эквалайзера с неограниченным числом ячеек возможно выбрать веса ячеек так, что 2)(с) О, т.е. q„=0 для всех п, исключая п = 0. Это значит, что МСИ может

быть полностью исключено. Величины весов ячеек для выполнения этой цели определяются из условия

о {пО)

Взяв г-преобразование от (10.2.5), получим

0(z) = C(z)F(z) = l

или просто

F(z)

(10.2.5)

(10.2.6)

(10.2.7)

где C(z) означает z-преобразование {с}. Заметим, что эквалайзер с передаточной функцией C(z) это просто обратный фильтр по отношению к линейной модели канального фильтра F(z). Другими словами, полное исключение МСИ требует использования фильтра, обратного F{z). Мы называем такой фильтр фильтром с нулевыми взаимными помехами («нуль-форсирующим» фильтром). Рис. 10 2.2 иллюстрирует блок-схему эквивалентного канала с дискретным временем и эквалайзера.

АБГШ

Рис. 10.2.2. Блок-схема канала с обнуляющим эквалайзером

Каскадное объединение обеляющего фильтра с передаточной функцией 1/F*(z") и эквалайзера с нулевыми взаимными помехами (ЭНВП) с передаточной функцией 1/F(z) приводит к эквивалентному ЭНВП с передаточной функцией

= .1. к - . (10.2.8)

как показано на рис. 10.2.3.

Этот комбинированный фильтр имеет на входе последовательность {ук} отсчётов согласованного фильтра, определённую (10.1.10). Его выход состоит из желательных символов, искажённых только аддитивным гауссовским белым шумом с нулевым средним. Импульсная характеристика комбинированного фильтра равна

(Л }

-►

Гауссовский шум

Эквиваленшин эквалаи-iep

Рис. 10.2.3. Блок-схема канала с эквивалентным обнуляющим эквалайзером

(10.2.9)

где интегрирование выполняется по замкнутому контуру, который содержит внутри себя область сходимости C(z). Поскольку X(z) - это полином с 2L корнями

Рз,... р, 1/р*, l/pj,... 1/р), то следует, что C(z) должен сходиться в плоскости, внутри единичной окружности (z = е*). Следовательно, контуром интегрирования может быть единичная окружность.

Качество эквалайзера с неограниченным числом ячеек, который полностью устраняет .МСИ, легко выразить через отношение сигнал-шум (ОСШ) на его выходе. Для математического удобства мы нормируем энергию принимаемого сигнала к единице. Это

предполагает, что f/o = 1 и что ожидаемая величина 4 также равна единице. Тогда ОСШ равно обратной величине дисперсии шума на выходе эквалайзера.

Величину al можно просто определить, если заметить, что шумовая последовательность {v.} на входе эквивалентного ЭНВП с характеристикой CXz) имеет нулевое среднее и спектральную плотность мошности

ФМ-М,Х{е), ш<.

(10 2.10)

где Х(е) получено из X{z) подстановкой z-e". Поскольку C() = 1/Jf(z), следует, что выходная шумовая последовательность эквалайзера имеет спектральную плотность .мошности

< -

Следовательно, дисперсия шума на выходе эквалайзера

а"=- *(<»)flfa) = 2я-«/г

а ОСШ на выходе ЭНВП равна

2к J

(10.2.11) (10.2.12)

(10.2.13)

Y(e"")

где индекс у у указывает на то, что эквалайзер имеет неограниченное число ячеек.

Спектральная характеристика Х(е"), соответствующая преобразованию Фурье последовательности отсчётов {х}, имеет интересную связь с характеристикой аналогового фильтра Я(ш), используемого в приёмнике. Поскольку

Эта нормировка используется во всей главе для математического удобства.