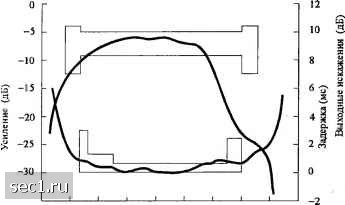35 О

-35 -

-40 -

СКО Г ФП

400 800 1200 1600 2000 2400 2800 3200 3600

Частота (Гц)

(а) Канал f большими амплитудными искажениями на краях диапазона

СКО ОФП

МСИ ОФП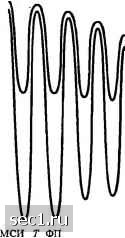

10 и

15 16 17 18 Время (символ ный И1 тервал)

(6) Качество эквалайзера

Рис. 10.2.7. Характеристики Т- и -гГ-эквалайзера для скорости 2400 символов в секунду

(ОФП означает отсутствие фильтра приёмника ФП) [Qureshi и Forney (1977), © 19771ЕЕЕ\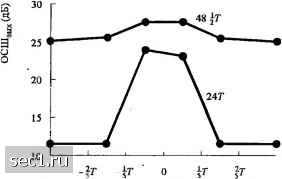

Отсчёты врем НИ

Рис. 10.2.8. Характеристики Т- и Т-эквалайзера для скорости 2400 символов в секунду при модуляции 16-КАМ в канале с пло.хой характеристикой ГВП [Gitlin и Weinstein (1981), ©\ШАТ8сТ\

Вход от согласованного фильтра

Прямой трансверсальный фильтр

Посимвольный детектор

Выходные данные -►

трансверсальный фильтр ОСР

Рис. 10.3.1. Структура эквалайзера с обратной связью по решению (ОСР)

Оба фильтра имеют ячейки, размещённые на символьном интервале Т. Входом для прямого фильтра является принимаемая символьная последовательность {о.). С учётом

этого прямой фильтр идентичен линейному .трансверсальному эквалайзеру, описанному в разделе 10.2. Фильтр обратной связи имеет на входе последовательность решений по предшествующим продетектированным символам. Функционально фильтр обратной связи используется для устранения в предстоящей оценке части МСИ, вызванной предыдущими продетектированны.ми символами.

10.3.1. Оптимизация коэффициентов

Из описанного выше следует, что выход эквалайзера можно выразить так

HA-j+Tjh-j, (10.3.1)

J=-K, y=i

где 4 - оценка к-го информационного символа, - коэффициенты ячеек фильтра, а Л \ -Jk A.j~" ранее продетектированные символы. Предполагается, что эквалайзер имеет {K + \) ячеек в своем блоке прямой связи и АГ, ячеек в блоке с обратной связью. Заметим, что этот эквалайзер нелинеен, поскольку фильтр обратной связи управляется предшествующими продетектированными символами {}.

Как критерий минимума пиковых искажений, так и критерий минимума СКО приводит к математически разрешаемой трактуемости оптимизации коэффициентов эквалайзера, как следует из статей Джорджа и других (1971), Прайса (1972), Сальца (1973) и Прокиса (1975). Поскольку критерий минимума СКО более распространен на практике, мы сосредоточим наше внимание на нём. Основываясь на предположении, что предшествующие продетектированные символы в цепи обратной связи приняты правильно, минимизация СКО

J(K„K,) = e\i,-I\\\ (10.3.2)

приводит к следующей системе линейных уравнений для коэффициентов в фильтре прямой связи:

(10.3.3)

4/0=1/:/,,.,-, +о5,, IJ-K,,-1, 0. (10.3.4)

Коэффициенты в фильтре обратной связи эквалайзера определяется через коэффициенты фильтра прямой связи следующим выражением:

.=-SsA-. k = \,2,...,K,. (10.3.5)

J- -fc>

Величины коэффициентов в блоке обратной связи приводят к полному исключению МСИ от предшествующих продетектированных символов в предположении, что предыдущие решения были правильными и что К L (см. задачу 10.9).

10.3.2. Качество эквалайзера с обратной связью по решению ЭОСР

Теперь сосредоточим наше внимание на качестве, достигаемом эквалайзером с обратной связью по решению. Точный расчет качества сложен при существовании

неправильных решений, сделанных детектором, которые затем распространяются по каналу обратной связи. При отсутствии ошибок в решениях получаем для минимума СКО

(10.3.6)

При переходе к пределу {K), когда число ячеек в фильтре прямой связи неограниченно, мы получаем наименьшую возможную СКО, обозначаемую У. При некоторых усилиях можно, как показано Сальцем (1973), выразить через

спектральные характеристики канала и аддитивного шума. Эта более приемлемая форма для J,„ определяется так:

I Т f/r

Xip") + N,

Соответствующее выходное ОСШ

1-Л.,

= -1 + ехр

fi/Г In я Т

N,+X(en N.

do .

(10.3.7)

(10.3.8) следовательно.

Снова видим, что при отсутствии МСИ X(q) = 1 и, m,n = 0 /(1 + о) • Соответствующее выходное ОСШ равно y=\/Na.

Пример 10.3.1. Интересно сравнить величину J для эквалайзера с обратной связью по решению с величиной J-, получаемой линейным эквалайзером с минимальной СКО. Например, рассмотрим эквивалент канала с дискретным временем, состоящий из двух ячеек с коэффициентами /, и /,. Минимальная СКО для этого канала равна

= ехр-

: ехр-! - In

= Nq ехр

[271 J, Ll + Afo+2/,y;cos(Q/ + 9)J 1

27C J

ln(l + No+ 2/o I/1 cosco)c/co

(10.3.9)

- 1 + 70+V(l + Ao)-4/o/,

Заметим, что максимизируется, когда /o = yiJ = Vi - Тогда

J 2iV„

™" l + iVo+V(l + Ao)-l

2N

7„«1.

Соответствующее выходное ОСШ

2N.

Nq«1.

(10.3.10)

(10.3.11)

Следовательно, имеется потеря в ОСШ на 3 дБ, обусловленная наличием МСИ. По сравнению с этим, потеря качества для линейного эквалайзера очень существенная. Его выходное ОСШ, определяемое (10.2.53), равно « (2/jVg)" для N«1.

Пример 10,3.2. Рассмотрим канал с экспоненциально затухающей импульсной характеристикой вида

/,=(\-а)"а\ = 0,1,2,...., (10.3.12)

где а < 1. Выходное ОСШ для эквалайзера с обратной связью по решению равно