Вхол

-ф Цх) Цх)

4 lijxo.l

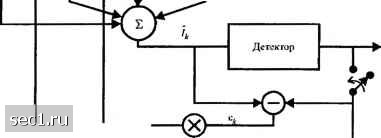ЧИ-4ZH4Zb--ЕЬ-

Piic. 11.1.1. Адаптивный эквалайзер с нулсвы.ми взаимны.\1И по.ч1с.\а\и1 (ЭНВП)

11.1.2. Алгоритм наименьших квадратов (НК)

При М1шимизац11и СКО, обсуждённой в разделе 10.2 2, мы нашли, что оптимальные коэффициенты эквалайзера определяются из решения системы линейных уравнений, выраженной в матричной форме;

ГС-, (11.1.6)

где Г - ковариационная матрица размером (2/ + l)x(2/< +1) отсчётов сигнала {и,}, С -

вектор-столбец из (2АГ + 1) коэффициентов эквалайзера, а -вектор-столбец канальны.ч

коэффициентов фильтра размерности (2/Г + 1). Решение для вектора коэффициентов С

оптимального эквалайзера можно получить путём обращения ковариационной матрицы Г, что можно эффективно выполнить посредством алгоритма Левинсона-Дурбина. описанного в приложении А.

Альтернативно для вычисления С можно использовать итеративную процедуру,

которая избегает обращение матрицы. Вероятно простейшая итеративная процедура - это метод крутого спуска, когда можно начинать выбором произвольного начального вектора С, скажем С„. Этот первоначальный выбор коэффициентов соответствует некоторой точке поверхности квадратичной функции СКО в пространстве коэффициентов размерности (2АГ + 1). Затем в этой точке на поверхности СКО вычисляется градиентный вектор Gn, имеющий 2АГ + 1 градиентных компонент \д.)1дс., к = -К,...,-],0,\...,К .

На каждом шаге вес меняется в направлении, противоположному соответствующе!! градиентной компоненте. Изменение веса на /-м шаге пропоршюнальио обьёму /-ой градиентной компоненты. Таким образом, последовательные значения коэффициентов С определяются согласно отношениям

C,,,=C,-AG„ =0,1,2,..., (11.1.7)

а вектор градиента равен

G, = = ГС, -? = V*) (И. 1.8)

Вектор С, представляет набор коэффициентов k-ii итерации, =/,-/, является сигналом ошибки на к-й итерации. V,-вектор отсчётов принимаемого сигнала, по

которым делаются оценки /, , т.е. V, -[и,;- ...и, ...и, .], а А - положительное число, выбираемое достаточно малым ля того, чтобы обеспечить сходимость итеративной процедуры. Если минимум СКО достигнут на некотором шаге к - к, тогда G, =0, так что дальнейшие изменения у шаговых весов не происходят. В обшем случае, при методе кратчайшего спуска точное значение -JiK) нельзя получить при конечных величинах

Однако, к нему можно как угодно приблизиться при некотором конечном значении к.

Принципиальная трудность метода кратчайшего спуска для определения оптимальных шаговых весов - это отсутствие знания вектора градиента G,, который зависит как от ковариационной матрицы Г, так и от вектора % взаимных корреляций. В свою очередь, эти величины зависят от коэффициентов {/,} эквивалентной модели канала с дискретным

временем и от ковариации информационной последовательности и аддитивного шума. Все эти величины могут быть, в общем, неизвестны на приёме. Чтобы преодолеть эти трудности, можно использовать оценку вектора градиентов. Это значит, что алгоритм настройки коэффициентов шаговых весов можно выразить в форме

c,„=c,-AG„ (11.1.9)

где G, означает оценку вектора градиентов G,, а С, означает оценку вектора коэффициента С,.

Из (11.1.8) мы замечаем, что G, равно обратной величине математического ожидания

8, V, , следовательно, оценка G, равна

G,=-s,v;. (11.1.10)

Поскольку /s(g,)=G,, оценка G, является несмещённой оценкой правильного вектора градиента G,. Подстановка (11.1.10) в (11.1.9) даёт алгоритм

c,„-c,+a£,v;. (11.1.11)

Это базовый алгоритм НК (наименьших квадратов) для рекуррентной настройки коэффициентов шаговых весов эквалайзера, впервые предложенный Уидроу и Хоффом (1960). Он иллюстрируется в эквалайзере, показанном на рис. 11.1.2.

Базовый алгоритм (11.1.11) и некоторые из его возможных вариантов были внедрены во многих коммерческих адаптивных эквалайзерах, которые используются в высокоскоростных модемах. Три варианта базового алгоритма были получены путём использования только информации о знаке, содержащейся в сигнале ошибки е, и (или) в

компонентах V,. Таким образом, три возможных варианта алгоритма определяются так •(t. 1)у = + csgn (8, )о* , 7 = - А,...,-1,0,1,..., А" (11.1.12)

с.,,,)-6-,+Ae,csgn(u* J, 7 = -.--1,0,1,...,/: (11.1.13)

"с.пу = S + Acsgn(s,)cssn(u* ), у = -/С, ...,-1,0,1,А, (11.1.14)

Вход {v}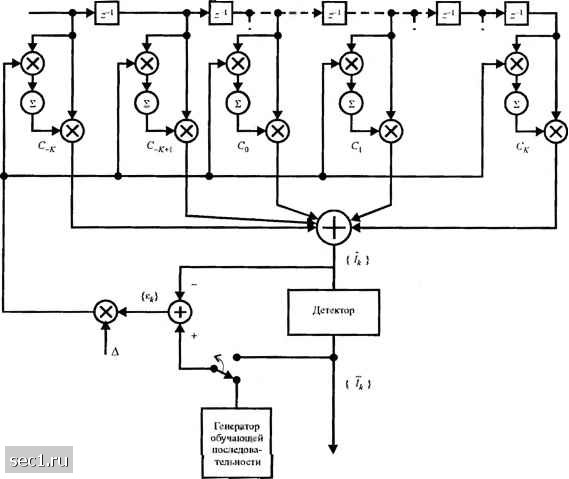

Ничач

Рис. 11.1.2. Линейный адаптивный экшыайзср, основанный на критерии миниллма СКО

где csgn(x-) определяется так

1 + 7 (Re(r) > 0,1т(л:) > 0),

1-у (Re(.Y)>0,Im(.Y)<0),

-1+7 (Re(x)<0,lm(x)>0),

csgn(.v) =

(11.1.15)

,-1-7 (Re(.r)<0,lm(x)<0), (Заметим, что в (11.1.15) j = V-T, что следует отличать от индекса7 в (11.1.12)-( 11.1.14)). Ясно, что алгоритм (11.1.14) реализуется существенно легче, но он дает наиболее медленную сходимость по сравнению с другими.

Несколько других вариантов алгоритма НК можно получить путем усреднения или фильтрации векторов градиентов по нескольким итерациям до выполнения настройки коэффициентов эквалайзера. Например, усреднение по векторам градиентов дает

J N i

(11.1.16)

a соответствующее рекуррентное уравнение для адаптации коэффициентов эквалайзера по Л итерациям имеет вид