Но это возможно тогда и только тогда, когда Ф..(/) О для всех/

Пример 2.2.1. Предположим, что фильтр нижних частот (ФНЧ), показанный на рис. 2.2 1. находится под воздействием случайного процесса X(t) со спектральной плотностью мощности

Ф«(/)2Ло для всех/ Случайный процесс с одинаковой спектральной плотностью на всех частотах называется белым шумом. Определим спектральную плотность мощности выходного процесса. Передаточная функция ФНЧ

/ ч Л 1

и, следовательно.

4{ft -

R + jlnfL \+JIk/L/R 1

\+(2nL/Ryf

(2.2.30)

R yiO

Рис. 2.2.1. Пример низкочастотного фильтра

Спектральная плотность мощности процесса на выходе

N. 1

2 l+(27tL/7?)V Эту спектральную плотность иллюстрирует рис. 2 2.2. Обратное преобразование Фурье определяет функцию автокорреляции

,2 -&df = t-*""-

(2.231)

(2.2.32)

•-"2 i+(2nL/Rff 4i

Автокорреляционная функция ф,у(т) показана на рис. 2.2.3. Заметим, что второй

момент процесса Y(t) равен фy(0) = RNqJAL .

В качестве заключительного упражнения определим взаимную корреляционную функцию между Y(t) и Д/), где Х(() - сигнал на входе, а У(/) - сигнал на выходе линейной системы. Имеем

Ф.v{/,,l) = e(y, Д;) = i\lh{a)e[x((,-a)x%)]ja =

Следовательно, случайные процессы Х(/) и /(/) совместно стационарны. Обозначив Irt2=x. имеем

ФЛх)£Ма)ф., (т-а)а. (2.2.33)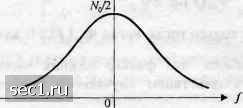

Рис. 2.2.2. Спектральная плотность мощности на выходе ФНЧ, когда на вход поступает белый шум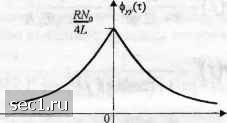

Рис. 2.2.3. Функция авгокорре.чяции сигшла на выходе ФНЧ, когда на вход поступает белый шум

Заметим, что интефал (2.2.33) - это интеграл свёртки. Следовательно, в частотной области из (2.2.33) следует соотношение

Ф>.(/)=Ф.«(/М/)- (2-2.34)

Видно, что если на входе системы действует белый шум, то функция взаимной корреляции входа и выхода системы с точностью до масштабирующего коэффициента равна импульсному отклику h(t).

2.2.4. Теорема отсчётов для частотно-ограниченных случайных процессов

Напомним, что детерминированный сигнал s(t) с преобразованием Фурье S(J) называется частотно-ограниченным, если S(f)=0 для \f\>W, где W - наивысшая частота, содержащаяся в s{i). Такой сигнал однозначно определяется отсчётами л(/), взятыми со скоростью/s> 2отсч./с. Минимальная скорость Д/ =2 отсч./с называется скорсктыо Найквиста. Представление сигнала через отсчёты, взятые со скоростью нилсе скорости Найквиста, ведёт к ошибкам.

Частотно-ограниченный сигнал, представленный отсчётами, взятыми со скоростью Найквиста, может быть восстановлен по своим отсчётам интерполяционной формулой

j\ ,,„,,sin[2HfK/-/7/2/-F)]

.sit)=Y.-nw) 2\,Kr-«/2F)

(2.2.35)

где {s(n/2W)} - отсчёты s(t), взятые в моменты времени t=nl2W, п=0, ±1, +2,.... Эквивалентным образом s(t) можно реконструировать путём пропускания отсчётов дискретизированного сигнала через идеальный ФНЧ с импульсной характеристикой h(i)=sin(2itWty2nWt. Рисунок 2.2.4 иллюстрирует процесс восстановления сигнала, основанный на идеальной интерполяции.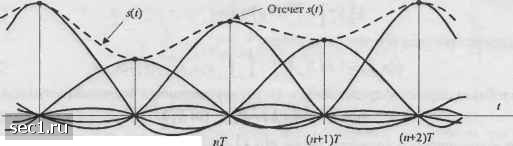

(«-2)Г

(/ь1)Г

Рис. 2.2.4. Восстановление сигнала основанное на идеальной интерполяции

Стационарный случайный процесс X(t) называется частотно-ограниченным, если его спектральная плотность мощности Ф(/)=0 для \J\>W. Поскольку Ф(/) является преобразованием Фурье автокорреляционной функции ф(т), то следует представление для ф(х):

Ф(х) = Е ф!

(2 2.36)

где {{nl2W)) - отсчёты ф(х), взятые при х -nllW, п=0, ±1, ±2.....

Теперь, если X(t) - частотно-ограниченный стационарный случайный процесс, то Х(() можно представить в виде

51п[2яЦ/-)

.2W.

(2.237)

где {X{nl2W)} - отсчёты Д/), взятые при tnl2W, и=0, ±1, ±2, ....

Это - представление стационарного случайного процесса через его отсчёты.

Отсчёты являются случайными величинами, которые описываются статистически соответствующей СФПВ. Представление (2.2.37) легко устанавливается доказательством того (задача 2.17), что

sin 2яЖ

i-wi

\2WJ

= 0.

(2.2.38)

Следовательно, равенство между представлением случайного процесса Х{() через его отсчёты и самого процесса понимается в том смысле, что средний квадрат ошибки равен нулю.

2.2.5. Случайные сигналы и системы с дискретным временем

Описание случайных сигналов с непрерывным временем, данное выше, можно легко распространить на случайные сигналы с дискретным временем. Такие сигналы обычно получаются путем равномерной дискретизации во времени случайного процесса с непрерывным временем.

Случайный процесс с дискретным временем Х{п) состоит из множества реализаций последовательностей {x(ri)}. Статистические свойства Х{п)=Х„ сходны с теми, которые определены для Х{(), с тем ограничением, что и теперь целая переменная (дискретное время). Следовательно, /w-и момент для Дн) определяется как