Выражение (11.1.30) можно упростить, если выбрать А так, что ДА,, « 1 для всех /с Тогда

Л « « imintrГ« Д(2/: + 1)J (X, + ;V„). (11.1.31)

Заметим, что х+М представляет принимаемый сигнал плюс мощность шума. Желательно иметь ./ < J, . Это значит, что А надо выбрать так, чтобы

«Д(2Л: + 1)(х,+„)<1.

или, что эквивалентно.

А<

(2K + \)(x,+N,) Для примера, если Д выбрать так:

(11.1.32)

(11.133)

(2а: + 1)(х-„+л,)

то уменьшение выходного ОСШ эквалайзера, обусловленное излишком СКО, меньше, чем 1 дБ.

Вышеприведённый анализ излишка среднеквадратичной ошибки базируется на предположении, что среднее значение коэффициентов эквалайзера сходится к оптимальной величине Ср,. При этом условии размер шага А удовлетворяет границе

(11.1.32). С другой стороны, мы определили, что сходимость векгора средних коэффициентов требует, чтобы А<2/Х . В то время как выбор Д вблизи верхней

границы 2/А,. может вести к начальной сходимости детерминированного (известного.)

градиентного алгоритма крутого спуска, такая большая величина Д обычно ведёт к нестабильности стохастического градиентного алгоритма НК.

Первоначальная сходимость или переходное поведение НК алгоритма была исследована различными исследователями. Их результаты ясно показывают, что размер шага должен быть уменьшен пропорционально длине эквалайзера, как следует из (11.1.32). Таким образом, верхняя граница, определяемая (11.1.32), также необходима, чтобы гарантировать первоначальную сходимость НК алгоритма. Статьи Гитлина и Вайнштейна (1979) и Унгербоека (1972) содержат анализ переходного поведения и свойства сходимости НК алгоритма.

Следующие примеры служат для подкрепления важных положений, высказанных выше, относительно первоначальной сходимости НК алгоритма.

Пример 11.1.1. НК алгоритм был использован для адаптивного выравнивания канала связи, для которого автокорреляционная матр1ща Г имеет разброс собственных значений /А,,. = 11. Число выбранных ячеек эквалайзера 2АГ-!-1 = 11 Входной сигнал плюс

.мощность шума x-t-N был нормирован к единице. Как следствие, верхняя граница для А, определяемая (11.1.32), равна 0,18. Рис. И. 1.4 иллюстрирует характеристики первоначальной сходимости НК алгоритма для Д= 0,045, 0,09 и 0,115 при усреднении оценок СКО по 200 опытам. Мы видим, что при выборе Д=0,09 (половина верхней границы) мы получаем относительно медленную сходимость. Если мы разделим Д на два до Д 0,045 скорость сходимости уменьшится, но излишек СКО также уменьшится, так что НК алгоритм работает лучше в стационарном режиме (при инвариантной во времени сигнальной среде). Наконец, мы отметим, что выбор Д=0,115, который ещё остаётся ниже

верхней границы, вызывает большие неи<елательные флуктуации выходной СКО алгоритма.

10

И 10 2 -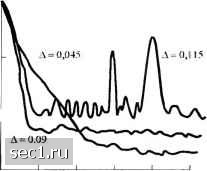

100 200 300 400 Чис.ю шорацин

Рис. 11.1.4. Характеристики первоначальной сходимости НСК алгорнт.ма при различных размерах шага. [Обработга цифровых сигналов. Дж.Дж.Прокис и ДДж.Монолакис, 1988J

При цифровой реализации НК алгоритма выбор параметра шага ячейки оказывается более критичным. В попытке уменьшить излишек СКО возможно уменьшить параметр размера шага ячейки до точки, когда суммарная СКО на самом деле увеличивается. Это условие возникает, когда оцененные градиентные компоненты вектора s, V,* после

умножения на малый параметр шага А оказывается меньше, чем половина наименьших значащих бита в фиксированной точке представления коэффициентов эквалайзера. В таком случае, адаптация прекращается. Следовательно, важно, чтобы размер шага ячейки был достаточно большим для того, чтобы удержать коэффициенты эквалайзера в окрестности С„,. Если желательно существенно уменьшить размер шага ячейки, то

необходимо увеличить точность коэффициентов эквалайзера. Типично, что для достаточно точного представления коэффициентов используется 16 бит, причем 10-12 наиболее значащих бита используется для арифметических операций по выравниванию сигнала Оставшиеся наименее значащие биты требуются для обеспечения необходимой точности процесса адаптации. Таким образом, масштабированные оцененные градиентные компоненты AsV, обычно влияют только на наименее значащие биты на любой итерации

В действительности, дополнительная точность также позволяет вести усреднение по шум, поскольку много нарастающих изменений в наименее значимых битах требуется до того, как возникнет изменение в верхних более значащих битах, используемых в арифметических операциях для выравнивания данных. Для анализа округлённых (случайных) ошибок цифровой реализации ЬЖ алгоритма читателю рекомендуются статьи Гитлина и Вайнштейна (1979), Гитлина и др. (1982) и Карайскоса и Лайу (1984).

Наконец, необходимо указать, что НК алгоритм годится и для отслеживания медленных, инвариантных во времени, статистик сигнала. В таком случае минимум СКО и оптимальный вектор коэффициентов будут переменны во времени. Другими словами •Aiiinl") является функцией времени и (2А+ l)-мерная поверхность ошибок передвигается с временным индексом . НК алгоритм пытается следить за изменением минимума •/„ „!/.) в (2А-1-1)-мерном пространстве, но он всегда запаздывает по отношению к значениям оцененных векторов градиента. Как следствие, НК алгоритм навлекает на себя другой вид

ошибок, называемых ошибками запаздывания, чьи значения средних квадратов уменьшаются с увеличением размера шага ячейки А. Суммарное СКО можно теперь выразить так

где означает средний квадрат ошибки, обусловленный запаздыванием. При заданной нестационарной адаптивной задаче выравнивания, если мы построим зависимости ошибок и J, от А, мы ожидаем поведение этих ошибок так, как показано на рис. 11.1.5. Видим,

что ./д увеличивается с ростом А, в то время как уменьшается с ростом А. Суммарная ошибка имеет минимум, который определяет оптимальный выбор параметра размера шага ячейки

Когда случайные изменения сигнала во времени происходят быстро, ошибка запаздывания будет определяющей для качества адаптивного эквалайзера. В таком случае »./т,„ даже тогда, когда используется наибольшее возможное значение А. Если это условие имеет место, НК алгоритм противопоказан для применения и необходимо для получения более быстрой сходимости и отслеживания рассчитывать на более сложные рекуррентные алгоритмы наименьших квадратов, описываемые в разд. 11.4.

Ср<.-Д11ий квадрат ошибки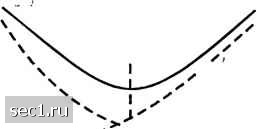

Ошибка, об>¥ловле11111Я зашумлсиними гр:дис1пами

J, Ошибка, обусловленная за11а;!Д1.1В.ием

*> .... за11а;!Д1.1В.11ие!1

-оЯ

Рис. 11.1.5. Зависимость излишка среднеквадратичной ошибки и ошибки-{ападдывания от размера шага ячейки. [Обработка цифровых сигналов. Дж.Дж.Прокис и Д.Дж.Манолакис., 1988]

11.1.5. Линейные эквалайзеры для базовых и полосовых сигналов

Наша трактовка адаптивных линейных эквалайзеров были выполнена через эквивалентные низкочастотные сигналы. Однако в практических приложениях адаптивный эквалайзер, показанный на рис.П. 1.2, можно реализовать или с базовыми или полосовыми сигналами. Например, рис.11.1.6 иллюстрирует демодуляцию сигналов КАМ (или многофазовый ФМ) при первоначальной передаче базовых сигналов и при выравнивании базовых сигналов при помощи эквалайзера с комплексными коэффициентами.

В действительности, комплексный эквалайзер с комплексными величинами (синфазных и квадратурных компонентов) по входу эквивалентен четырём параллельным эквалайзерам с вещественными коэффициентами ячеек, как показано на рис.11.1.7.

В качестве альтернативы, мы можем выравнивать сигнал как полосовой. Это выполняется, так, как показано на рис.11.1.8 для двухмерного сигнального созвездия как при КАМ и ФМ. Принимаемый сигнал фильтрируется и. параллельно, он проходит через преобразователь Гильберта, называемый фазо-расгцепляющим фильтром.