декодеру Витерби, можно преодолеть путём введения идентичной задержки в настраиваемых весах ячеек для коэффициентов эквалайзера, как показано на рис. 11.2.3. Основную цену, которую нужно платить за дополнительную задержку сводится к уменьшению параметра размера шага в алгоритме НК, для достижения стабильности алгоритма, как описано Лонгом и др.(1987, 1989).

Сигтш ошибки

Огсч II.1 припим leMoio

Ад.<11ТИ!11МЙ ЛИИ ин jfi эквалайюр

3sUKp>KKa

Декодер Ии гсрби

Рошсиня

Рис.11.2.3. Настрой! эккыайзсра, основанного на решениях декодера

В каналах с одним или большим числом спектральных нулей по по1юсе частот, когда линейный эквалайзер не годится для компенсации канальной МСИ, мы используем ЭОСР. Но ЭОСР требует надёжные решения в своём фильтре обратной связи для того, чтобы погасить МСИ от предварительно продетектированных символов. Предварительные решения до декодирования в большей степени ненадёжны и, следовательно, не подходящие. К сожалению, общепринятый ЭОСР не может быть каскадно соединён с алгоритмом Витерби, чтобы решение после декодера вернуть по цепи обратной связи в ЭОСР.

Данные

Колер

Перемежи го.п.

Mo,(>jbiiop

И МИ1.Ъ1 -►

(я) Переда I чны

принимаемого

Эквашйзер с прямой

Деиерсмсжител!.

Задержка

(А) Приёмник-

Декодер Вик-рби

Решения

Фильтр обратной сви <и (рел1К.п.1теЛ1.)

Рис.11.2.4. Использование ЭОСР с предсказанием с перемежсние.м и решёточно-кодовой модуляцией

Одна альтернатива сводится к использованию ЭОСР с предсказанием, описанного в разд. 10.3.3. Для того, чтобы приспособиться к задержке при декодировании, поскольку она влияет на линейный предсказатель, мы вводим в систему периодическую пару перемежитель-деперемежитель, которые имеют ту же задержку, что и декодер Витерби, и

таким образом делают возможным генерировать соответствующий сигнал ошибки для предсказателя, как показано на блок-схеме рис. 11.2.4.

Новый путь комбинирования ЭОСР с предсказанием с декодером Витерби для выравнивания решётчато-кодированых сигналов описан и проанализирован Эйбоглу (1988). Та же идея использована для выравнивания многопутевых каналов с замираниями Зоу и др. (1988, 1990), но структура ЭОСР была модифицирована для использования рекурсивных минимально-квадратичных лестничных фильтров, которые обеспечивают более быструю адаптацию к изменениям во времени, возникающим в канале.

11.3. АДАПТИВНЫЙ ОЦЕНИВАТЕЛЬ КАНАЛА ДЛЯ МАКСИМАЛЬНО

ПРАВДОПОДОБНОГО ПОСЛЕДОВАТЕЛЬНОГО ДЕТЕКТИРОВАНИЯ

Правило МП последовательного детектирования, реализованное алгоритмом Витерби, воплощенное в расчёте метрик (10.1.23), и вероятностный алгоритм посимвольного детектирования, описанный в разделе 5.1.5, требуют знания коэффициентов [/,

эквивалентного канала с дискретным временем. Чтобы приспособить их к неизвестному каналу или каналу с медленными изменениями во времени, можно включить оцениватель канала, работающий параллельно с алгоритмом детектирования, как показано на рис.11.3.2.

Оцениватель канала, показанный на рис.11.3.2 идентичен по структуре линейному трансверсальному эквалайзеру, обсужденному ранее в разделе 11.1.

Вход {и,}

Алгоритм Витерби

/; ВЫ.ХОД

Оценка канала

Оцепиваталь канала

Рис. 11.3.1. Блок- с.чема метода оценивания .характеристик канала для алгоритма Витерби

Действительно, такой оцениватель канала является воплощением (replica?) эквивалентного канала с дискретным временем, который моделирует МСИ. Оцененные

коэффициенты ячеек, обозначаемые (/, }, подстраиваются рекуррентно для минимизации СКО между действительно принимаемой последовательностью и выходом оценивателя. Для примера, алгоритм кратчайшего спуска в варианте выполнения операций с управлением решениями можно записать так:

L,=f,+A8j;, (113.1)

где f, - вектор коэффициентов усиления ячеек на -й итерации, А-размер шага ячейки, 8, - и, - и, - сигнал ошибки, а I, означает вектор детектированных информационных символов в оценивателе канала на к-й итерации.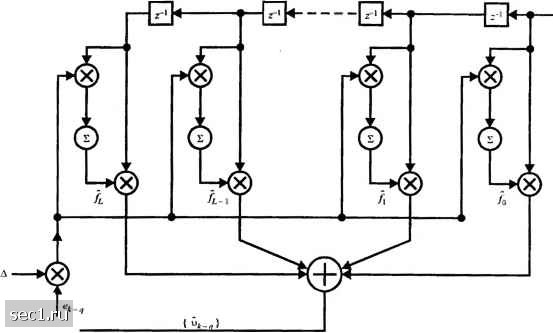

Рис. 11.3.2. Адаптивный трансверсальный фильтр для оценивания канального рассеяния

Теперь покажем, что когда СКО между и и, минимизируется, результирующие

значения коэффициентов усиления ячеек оценивателя канала являются величинами модели канала с дискретным временем. Для математической трактуемости предположим, что

правильная, то есть

продетектированная информационная последовательность идентична переданной последовательности (/,.}. Это разумное предполоисение, когда система работает при малой вероятности ошибок. Таким образом, СКО между

принимаемым сигналом и, и оценкой и, равна

J(f) = E

(11.3.2)

Коэффициенты ячеек {/], которые минимизируют j{f ) в (11.3.2), удовлетворяют системе из линейных уравнений

(11 3.3)

л- I

(11.3.4)

Из (11.3.3) и (11.3.4) следует, что пока информационная последовательность некоррелирована, оптимальные коэффициенты точно равны соответствующим величинам эквивалентного канала дискретного времени. Также очевидно, что когда число ячеек оценивателя канала больше или равно L + \, оптимальные коэффициенты усиления ячеек