имеем

(t) = - [P; -1) - (OYJCOP (/ - l)IwD,, (/ -1) + /(/)Y;(0]

: (/ - 1)D (/ -1) + -/(ОРл, (i - 1)Y; (/)

-k(0y;J(0p(/-i)d/-i) --/(Ok(/)y(OP;,(/-i)y;(/)

= C(t-l) + K(0[/(0-Y(OC(/-l)] (11.4.17)

Заметим, что \l(t)C(t-V) это выход эквалайзера в момент /, то есть

/(/) = Y;(/)C(/-1) (11.4.18)

e(t,t-l) = I(t)-I(t)e(t) (11.4.19) -это ошибка между желательным символом и его оценкой. Таким образом, C,(/) определяется рекуррентно согласно отношению

(О = Q -1) + (О (/). (11.4.20) Остаточный СКО, получаемый при такой оптимизации, равен

KZ. - i:" I («) \" ~ci(f)K(o. (11.4.21)

Для суммирования предположим, что мы имеем C,(/-l) и P,(/-l). Когда принимается новая сигнальная компонента имеем Уд,(/). Затем рекуррентные вычисления для обновления C(i) и P(t) продолжаются так:

- вычисляется выход:

- вычисляется ошибка:

л, (О = /(0-/(0,

- вычисляется вектор калмановского усиления:

К (Л- P;.(-OYj(/) " w + YJ(/)P(/-1)Y;(/)

- вычисляется соотношение обратных матриц

Р;. (О = [Р (/ -1) - (/)Y (/)Р (t -1)],

- определяются коэффициенты

(/) = С (Г -1) + (/)е (/) - С (/ -1) + (/)Y; (t)e (О - (11-4 22)

Алгоритм, определяемый (11.4.22), назван прямой формой РЬЖ или алгоритмом Калмана. Он подходит, когда эквалайзер имеет трансверсальную (прямая форма) структуру. Заметим, что коэффициенты эквалайзера меняются со временем на величину, равной ошибки е(0, уменьшенной на вектор усиления Калмана К;(/). Поскольку Kf(t) является Л/-мерным каждый коэффициент ячейки в действительности управляется одним из элементов Кд, (/). Как следствие получается быстрая сходимость. В противоположность

этому, алгоритм кратчайшего спуска, выраженный в новых обозначениях, определяется так

С„ (() = С„ (/-!) + (11.4.23)

и единственным переменным параметром является размер шага ячейки Д.

Рис. 11.4.1 иллюстрирует начальную скорость сходимости этих двух алгоритмов для канала с фиксируемыми параметрами /о = 0,26, / = 0,93, /, = 0,26 и линейного эквалайзера с 11 ячейками. Отношение собственных значений для этого канала

/=11. Все коэффициенты эквалайзера были первоначально обнулены. Алгоритм кратчайшего спуска был реализован с А - 0,020. Превосходство алгоритма Калмана очевидно. Это особенно важно при отслеживании меняющегося во времени канала. Для примера, изменения во времени высокочастотного (ВЧ или KB) ионосферного радиоканала слишком быстрые, чтобы их выравнивать градиентным алгоритмом, но алгоритм Кальмана адаптируется достаточно быстро для отслеживания таких изменений.

Несмотря на прекрасные качества отслеживания алгоритм Калмана, описанный выше, имеет два недостатка. Один - его сложность, второй - его чувствительность к случайному шуму, который накапливается при рекуррентных операциях. Последний может вызвать нестабильность алгоритма.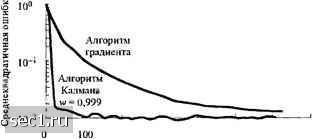

200 300 400 500 600 700 Число итераций

Рис. 11 4.1. Сравнение скорости сходимости а-тгоритш! Калмана и градиентного алгоритма.

Число вычислений или операций (умножений, делений и вычитаний) при расчете величин (11.4.22), пропорционально Л. Большинство из этих операций используется при определении Р,(/). Эта часть вычислений также чувствительна к случайному шуму. Чтобы

решить эту проблему были разработаны алгоритмы, которые избегают вычисления Ру(0 согласно (11.4.14). Основа этих алгоритмов сводится к декомпозиции Рд,(/) в виде

PAf) = %mAfKiO, (И.4.24)

где 8,Д0- нижняя треугольная матрица, чьи диагональные элементы - единицы, а Ад,(/) диагональная матрица. Такая декомпозиция называется факторизачиеь (см. Бирман, 1977). Эта факторизация описывается в приложении D. В алгоритме факторизации Р (/) не обновляется, как в (11.4.14), а вычисляется. Вместо этого при помощи рекуррентного обновления формируются S, (/) и Л (/) .

Алгоритмы НК часто используются в системах управления, которые включают в себя калмановскую фильтрацию. В цифровой связи, алгоритм НК Калмана используется в ФМ модеме с выравниванием на основе обратной связи по решению, спроектированном для передачи с высокой скоростью по ВЧ каналу с номинальной полосой частот 3 кГц. Этот алгоритм описан в статье Хшу (1982). Он имеет вычислительную сложность порядка ISN-6,SN (умножения комплексных величин и делений на выходные символы) Хпя

подробного ознакомления с алгоритмами НК в последовательном оценивании читателю рекомендуется книга Бирмана (1977).

Возможно также разработать РНК алгоритмы с вычислительной сложностью, которая возрастает линейно с числом коэффициентов эквалайзера N. Такие алгоритмы обычно называются быстрыми РНК алгорит.мами, и они были описаны в статьях Караяниса и др. (1983), Чиффи и Кайлата (1989) и Слока и Кайлата (1988).

11.4.2. Линейное предсказание и лестничные фильтры

В главе 3 мы рассмотрели линейное предсказание сигнала в плане кодирования речи. В этом разделе мы хотим установить связь межу линейным предсказанием и лестничным фильтром.

Проблему линейного предсказания можно сформулировать так; по значениям набора данных y{t-\),y{i-2),...,у{/-р) надо предсказать значение данных в последующей точке у(/). Предсказатель порядкар определяется так

У 0) = i,,yi-fc). (11.4.25)

Минимизация СКО

<р = Чу(П~у (О

(11.4.26)

по коэффициентам предсказания {я,} ведет к системе линейных уравнений

Ха,Ж-/) = Ф(/), / = 1,2,...,/;, (11.4 27)

т=Е[у(оуо+п].

Их называют иор.мальны.ми уравнсниялт Ю.пи-Волкера.

Матрица коэффициентов Ф с элементами ф(/г-/) является тёплицевой матрицей.

Следовательно, алгоритм Левинсона-Дурбина, описанный в приложения А, дает эффективный способ для рекуррентного решения линейных уравнений, начиная с предсказателя первого порядка и продолжая рекуррентно для нахождения коэффициентов предсказателя порядка р. Рекуррентные соотношения для алгоритма Левинсона-Дурбина таковы

«и=, п=Ф(0) " ф(0) "

(11.4 28)

2

для т - \,2,...,р , причём векторы А„, , ф, j определены так:

ф:-,=[ф("-1) ф("-2) ... ф(1)Г

Линейный предсказывающий фильтр порядка т можно реализовать как трансверсальный фильтр с передаточной функцией