Его входом являются данные {у(0}, го выходом - ошибка е(0 = 3(0" i(О Предсказывающий фильтр можно также реализовать в лестничном виде, как мы теперь покажем.

Начнём с использования алгоритма Левинсона-Дурбина для коэффициентов предсказателя в (11.4.29). Подстановка даёт

/и-1

т-\ f т I \

t-1 V J

= "Чм()- (11.4.30)

Таким образом, мы получили передаточную функцию предсказателя /?ьго порядка через передаточную функцию {т-\)-то порядка. Теперь предположим, что мы определяем фильтр с передаточной функцией (j„,() > равной

G„,(z) = z-"J")- (11.4.31)

Тогда (11.4.30) можно выразить так

A„X)-A,„,{z)-a„,„,zG„,,X-A. (114.32)

Заметим, что G„, ,(z) представляет трансверсальный фильтр с коэффициентами в отводах (-я„, , ,-а,„ , ,„ ,... ,,, 1), в то время как коэффициенты для А , (z) такие же

за исключением того, что они даны в обратном порядке.

Больше понимания соотношения между /l„,(z) и (j,„(2) можно получить путем вычисления выхода этих двух фильтров при подачи ко входу последовательности y{f). Используя г-преобразование, имеем

A,Sz)Y{z) = A„, Xmz)-a„„„z-G„, Xm d 1-4.33) Выходы фильтров мы определяем так

РЛАЛт (,,.4.34)

Тогда (11.4.33) можно записать

РЛ) = КХ)-с„.„,г "5„,.,(z). (11.4.35)

Во временной области соотношение (11.4.35) можно выразить так

Ш - л,-, (О - «„,„,б„,, (/ -1), /" > 1. (11.4.36)

Л(0 = ЯО-Е«..Я/-). (114.37)

к (О -y(fn,)Y. "« -+ ) - (114-38)

»-1

Для детальной разработки отметим, что /„,(/) в (11.4.37) представляет ошибку предсказания w-ro порядка по более ранним отсчётам (ошибка вперёд), в то время как /»„,(/) представляет ошибку предсказания т-го порядка по более поздним отсчетам

(ошибка назад).

Соотношение (11.4.36) - одно из двух, определяющих лестничный фильтр. Второе соотношение получается из G„,(z) следующим образом:

0Л) = = "Л(") = ""К-.(-)-)] = -G„. ,iz)-a„,„A,,(z). (11.4.39) Теперь мы умножим левую и правые части (11.4.39) на Y(z) и выразим результаты через F{z) и B(z), используя определение (11.4.34), мы получим

BM = z-B„ ,iz)-a„„F„ ,{z). (11.4.40)

Путем преобразования (11.4.40) во временную область мы получим второе отношение, которое соответствует лестничному фильтру, а именно

Ь„(0 = 1)-«.„.Л-,(0, 1 (11.4.41)

Начальные условия

Л(0 = Ь,(() = У(0. (11.4.42)

Лестничные фильтры, описанные рекуррентными отношениями (11.4.36) и (11.4.40), иллюстрируются на рис. 11.4.2.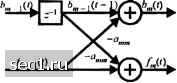

Каскад 1

*i(0

-►

Каскад 2

---►

Рис. 11.4.2. Лестничный фильтр.

Каждый каскад характеризуется собственным коэффициентом умножения {а j, / - l,2,...,.iV. который определяются алгоритмом Левинсона-Дурбина. Ошибки вперед и назад /„ХО и Л«(0 обычно называют t»cwa/w/aw . Средний квадрат этих остатков равен

blit)

а <f.„ определяется рекуррентно согласно алгоритму Левинсона-Дурбина:

г»=!™-.0-«1,) = ?оП(1-а,),

(11.4.43) (11.4.44)

<?,=ф(0).

Остатки {/„,(0} и удовлетворяют ряду интересных свойств, как описано

Макхоулом (1978). Наиболее важные из них - свойства ортогональности

£к(Об„(о]=„,5„,„,

Далее, взаимные корреляции между /„(О и 6„(/) определяются так

(11.4.45)

10 (jn < п)

(11.4.46)

Вследствие свойств ортогональности остатков, различные секции лестницы проявляют форму независимости, которая позволяет нам прибавить или удалить одну или больше последних каскадов без влияния на параметры оставшихся каскадов. Поскольку остаточный средний квадрат ошибки iS уменьшается монотонно с числом секций,

можно использовать как показатель качества того, каким числом ячеек можно ограничиться.

Из вышеприведенного обсуждения мы видим, что линейный предсказывающий фильтр можно реализовать или как линейный трансверсальный фпльтр или как лестничньн"! фильтр. Лестничный фильтр рекуррентен по порядку и, как следствие, число его секций (каскадов) можно легко увеличить или уменьшить без влияния на параметры оставшихся секций. В противоположность этому коэффициенты трансверсального фильтра, полученные на основе РЖ, взаимозависимы. Это значит, что увеличение или уменьшение размера фильтра приведет к изменению всех коэффициентов. Следовательно, алгоритм Калмана, описанный в разделе 11.4.1, рекуррентен во времени, но не по порядку реализующих его звеньев.

Основываясь на оптимизации по критерию наименьших квадратов, лестничные алгоритмы РЬЖ были разработаны так, что их вычислительная сложность растет линейно с ростом числа коэффициентов фильтра N (числа каскадов). Таким образом, структура лестничного эквалайзера в вычислительном отношении конкурентоспособна с алгоритмом быстрого РНК эквалайзера прямой формы. Лестничные алгоритмы РЬЖ описаны в статьях Морфа и др. (1973), Саториуса и Александера (1979). Саториуса и Пака (1981), Линга и Прокиса (1984) и Линга и др. (1986).

Лестничные алгоритмы РНК имеют несомненное будущее, поскольку они численно нечувствительны по отношению к случайным ошибкам, свойственным цифровой реализации алгоритма. Трактовку их количественных характеристик можно найти в статьях Линга и других (1984, 1986).

11.5. СЛЕПОЕ ВЫРАВНИВАНИЕ

В общепринятых эквалайзерах, работающих по алгоритму сведения к нулю или минимума СКО, мы предположили, что к приёмнику передаётся известная обучающая последовательность для целей начальной настройки коэффициентов эквалайзера. Однако имеется ряд приложений, таких как многопользовательские сети связи, когда желательно для приёмника синхронизироваться от принимаемого сигнала и настроить эквалайзер без использования обучающей последовательности.

Техника выравнивания, основанная на первоначальной настройке коэффициентов без использования обучающей последовательности, названа самонастраивающейся или c.ieuoU.

Начиная со статьи Сато (1975), за последние два десятилетня были разработаны три различных класса адаптивных алгоритмов слепого выравнивания. Один класс алгоритмов основан на методе кратчайшего спуска для адаптации эквалайзера. Второй класс алгоритмов основан на использовании статистики второго и более высокого порядка (обычно четвёртого порядка) принимаемого сигнала для оценки начальных характеристик и синтеза эквалайзера. Совсем недавно был изобретён третий класс алгоритмов слепого выравнивания, основанный на правиле максимального правдоподобия. В этом разделе мы вкратце опишем эти подходы и дадим несколько относящихся к теме ссылок на литературу.

11.5.1. Слепое выравнивание, основанное на критерии максимального правдоподобия

Удобно использовать эквивалентную модель канала с дискретным временем, описанную в разделе 10.1.2. Напомним, что выход этой модели канала с МСИ равен