Yn = g„, и-1,2,...,!

(12.1.8)

Если оценки получены при наблюдении принимаемого сигнала по одному или

многим сигнальным интервалам, как описано в приложении С, их статистические характеристики описываются гауссовским распределением. Тогда характеризуются

как взаимно независимые и одинаково распределенные гауссовские случайные величины. Такие же свойства у величин {„} Как при некогерентном детектировании, мы допускаем корреляцию между и }, но не между Jf„, и для тп.

12.1.1. Двоичные сигналы

В приложении В мы получили вероятность того, что общая квадратичная форма

0 = ЪЛХ„ г- +ВI F„ +CXJ: +CXJ,:) (12.1 9)

i»=i

комплексных гауссовских случайных величин меньше нуля.

Эта вероятность, которая дана формулой (В.21) приложения В-это вероятность ошибки двоичной многоканальной передачи в каналах с АБГШ. Определённое число частных случаев имеет важное значение.

Если двоичные сигналы противоположны, а оценки точные, как при когерентной ФМ вероятность ошибки определяется простейшей формулой

Pb = Q[X (12.1.10)

Nq „ ] Na „ 1

- ОСШ на бит. Если все каналы идентичны а„ а для всех и, следовательно,

У, = -а-. (12.1.12)

Видим, что Z,g- это общая энергия L переданных сигналов. Интерпретация этих результатов сводится к тому, что приёмник складывает энергии L каналов оптимальным образом. Это значит, что нет потери качества при делении суммарной энергии переданных сигналов по L каналам. Такое же качество будет в случае, когда единственный сигнал с энергией Ls передается по одному каналу. Такое поведение имеет место только, если оценка точная g„ - g„ для всех «. Если оценки неправильные, то возникает потеря в

качестве, величина которой зависит от качества оценки, что описывается в приложении С. Точные оценки } соответствуют экстремальному случаю. В другом экстремальном

случае мы имеем двоичную ДФМ. В ДФМ оценки „ } являются просто нормированными

отсчётами сигнала в смеси с шумом на выходе согласованных фильтров на предыдущем сигнальном интервале. Это наихудшая оценка, которую можно рассмотреть, используя оценки {g. Для двоичной ДФМ вероятность ошибки, следующая из (В.21), равна

Pb = lelLcSb. (12.1.13)

где, по определению,

2 JL-l-n

(12.1.14)

2Z,-r

и v,- ОСШ на бит, определенное (12-1-11), а для идентичных каналов в (12.1.12). Этот результат можно сравнить с вероятностью ошибки при использовании одного канала (L = l). Для упрощения сравнения мы предположим, что L каналов имеют одинаковые множители ослабления. При том же значении у, качество многоканальной системы хуже

одноканальной. Это значит что распределение общей переданной энергии по L каналам ведет к потере качества, величина которой зависит от L .

Потеря в качестве также возникает при квадратичном детектировании ортогональных сигналов, переданных по L каналам. Для двоичных ортогональных сигналов выражение для вероятности ошибки идентично по форме той, что для двоичной ДФМ, данное в (12-1-13), исключая того, что заменяется на у. Это значит, что двоичные

ортогональные сигналы при некогерентном детектировании на 3 Дц хуже, чем двоичная ДФМ. Однако потеря в качестве, обусловленная некогерентным сложением сигналов, принимаемых по L каналам идентична той, что для двоичной ДФМ.

Рис. 12.1.1 иллюстрирует потери, обусловленные некогерентным (квадратичным) сложением L сигналов, как функция от L .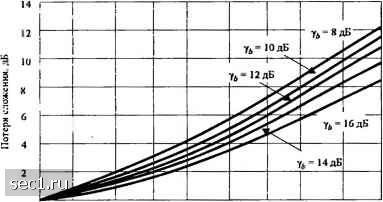

100 200 500 1000

Число каналов, l

Рис. 12.1.1. Потери сложения при некогерентном детектировании и сложении двоичных многоканальных сигналов

Вероятность ошибки на рисунке не показана, но её легко определить по формуле

PbW", (12.1.15)

которая определяет вероятность ошибки двоичной ДФМ, показанная на рис.5.2.12. Затем определяются изменения требуемого ОСШ на бит, у, при учёте

потерь некогерентного

сложения, соответствующие данной величине L.

12.1.2. М-ичные ортогональные сигналы

Теперь рассмотрим Л/-ичные ортогональные сигналы с квадратичным детектированием и сложением сигналов L каналов. Величины для решения определяются (12-1-4). Предположим, что сигналы sj"\t\ н = 1,2,..., L, переданы по L каналам с АБГШ. 1 Тогда величины для решения выражаются так:

(12.1.16)

комплексные гауссовские случайные величины с нулевым средним и

дисперсией = е{!\1 „„У-ISNg. Поэтому /7, описывается статистически нецентральным хи-квадрат распределением с 2L степенями свободы и параметром нецентральности

s = J:(2na.y=4ntoLl (12.1.17)

Используя (2.1.17), получим для ФПВ

/2 X

ft-i

2ПЫо

г/, >0.

(12.1.18)

С другой стороны, распределением {u„\ w = 2,3,...,Л/ статистически независимые

и одинаково распределённые случайные величины с центральным хи-квадрат распределением с 2L степенями свободы для каждой. Используя (2.1.10), мы получаем ФПВ для

« >0, «1 = 2, 3,...,М.(12.1.19)

Вероятность ошибочного приёма

Pm = i-Pc = -p(U2<UuU3<Uu.....,им<ид=

= \-[[P(U2<m\U = м.)Г"р(«.)м,.

PiUi < wi I f/i = Ml) = 1 - ехр Таким образом

PM=i-h-e"""j:l,

о L к-О

Z 1-1 It

пЧ к=0 f!.

(12.1.20)

(12.1.21)

i-i ..*-Vu(-)/

V ГУ

Piui)di4i -"V.-i(2Vy),

(12.1.22)

7 = Sa/o-

Интеграл в (12.1.22) можно вычислить численно. Возможно также разложить (1-х) в (12.1.22) в ряд и выполнить интегрирование почленно. Такой подход дает выражение для Р через ограниченные суммы.

Альтернативный подход сводится к использованию объединённой границы

P<(M-1)P,(L), (12.1.23)

где P-.{L) - вероятность ошибки при выборе вместо f/, одну из М -1 величин для решения [{/Д /и = 2,3,...,М. С учётом нашего предыдущего обсуждения качества двоичной ортогональной системы сигналов, имеем

(12.1.24)

где с„ определяется (12.1.14). При относительно малых значениях М, объединённая граница в (12-1-23) достаточно плотная для большинства практических приложений.