
 | |
|
НПО Системы Безопасности (499)340-94-73 График работы: ПН-ПТ: 10:00-19:00 СБ-ВС: выходной  |
Главная » Периодика » Безопасность 0 ... 190191192193194195196 ... 262 12.2. связь со многими несущими Из нашей трактовки неидеальных линейных фильтровых каналов в главах 10 и II мы видели, что такие каналы приводят к МСИ, которая ухудшает качество по сравнению с идеальным каналом. Степень ухудшения качества зависит от частотной характеристики канала. Далее, сложность приёмника увеличивается по мере увеличения протяжённости МСИ. При заданной частотной характеристике канала разработчик системы связи должен решать, как эффективно использовать имеющуюся полосу частот канала для надёжной передачи информации в пределах ограничений на мощность передатчика и сложности приемника. Для неидеального линейного фильтрового канала один из выборов сводится к использованию системы с одной несущей, в которой информационная последовательность передаётся последовательно с некоторой определённой скоростью R символов/бит. В таком канале время рассеивания обычно намного больше, чем символьный интервал и, следовательно возникает МСИ из-за неидеальной частотной характеристики канала. Как мы уже отметили ранее, в этом случае необходим эквалайзер для компенсации искажении в канале. Альтернативный подход к синтезу частотно-эффективной системы связи при наличии искажений в канале сводится к разделению имеющейся в распоряжении полосы частот на определенное число подканалов так, что каждый подканал почти идеален. Для детальной проработки предположим, что С(/)-это частотная характеристика неидеального частотно-ограниченного канала с полосой W и что спектральная плотность мощности аддитивного гауссовского шума Ф„„(/)- Затем мы делим полосу W на N = IV/AJ подканалов с шириной А /, где А / выбирается достаточно малой, так что /фпп{/) примерно постоянно в пределах каждого подканала. Далее мы хотим выбрать распределение мощности переданного сигнала по частоте P(f) так, чтобы удовлетворять ограничению \P(J)df<p, . (12.2.1) где - имеющаяся в распоряжении средняя мощность передатчика. Определим пропускную способность неидеального канала с аддитивным гауссовским шумом. 12.2.1. Пропускная способность неидеального линейного фиксированного канала Напомним, что пропускная способность идеального, частотно-ограниченного, канала с АБГШ равна C = W\og. Р Л (12 2.2) где С- пропускная способность в бит/с, W- полоса канала, а р<.р-средняя мощность переданного сигнала. В системе с многими несущими с достаточно малой величиной Д/ пропускная способность подканала А/ра)с(/)Г А/Ф„„а) Тогда суммарная пропускная способность канала P{l)\c{.f.y- С, = A/log, 1 + - (12.2.3) С = i;C. = A/flog, 1 + - (12.2.4) в пределе, когда А/" О, мы получим пропускную способность в бит/с: Pjf) C(ff (12.2.5) С учётом ограничений на P{J), определяемые (12.2.1) выбор P(f), который максимизирует С, можно сделать путем максимизации интеграла Р(ЛС(/У log: 1 + - +xp(nW, (12.2.6) Ф„.(/) J где А,- множитель Лагранжа, который выбирается так, чтобы удовлетворить заданному ограничению (12.2.1). Используя метод вариации для обеспечения максимизации, мы находим, что оптимальное распределение мощности переданного сигнала определяется решением уравнения - + Х = 0. (12.2.7) С(Л Р(Л + ФпМ) Следовательно, Д/)+Ф„„(/)/С(/)" должна быть константой (К), чья величина подстраивается с тем, чтобы удовлетворить ограничению на среднюю мощность (12.2.1). Это значит, что [о (fW). (12.2.8) Выражение для пропускной способности неидеального линейного фильтрового канала с АБГШ принадлежит Шеннону (1949). Фундаментальная интерпретация этого результата сводится к тому, что мощность сигнала должна быть велика, когда канальное ОСШ С(/)Р/ф„„(/) велико, она должны быть мала, когда ОСШ мало. Этот результат о распределении переданной мощности иллюстрируется на рис. 12.2.1. 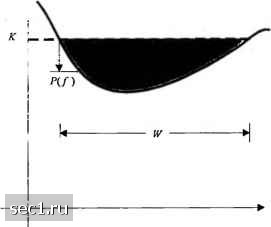 Частота Г Рис. 12.2.1. Оптимальный спектр: иллюстрация решения с помощью заполнения чаши водой Видим, что если Ф„„(/)/С(/)Г интерпретировать как дно чаши единичной глубины и мы налили определенное количество воды равное рр в чашу, вода сама распределится по чаше так чтобы достичь пропускную способность. Это называется водо-наполняемая интерпретация оптимального распределения мощности, как функции частоты. Интересно отметить, что пропускная способность наименьшая, когда канальное ОСШ 1С(/)Р/ф„„(/) является константой для всех f . В этом случае /*(/) - константа для всех f . Эквивалентно, если частотная характеристика канала идеальная, т.е. С(/) = 1 для f , тогда наихудшее распределение мощности гауссовского шума, с точки зрения максимизации пропускной способности, соответствует белому гауссовскому шуму. Вышеизложенное наводит на мысль, что передача со многими несущими, при которой доступная полоса канала делится на подполоски с относительно узкой полосой А/" = WlN, даёт решение, которое может обеспечить скорость передачи, близкую к пропускной способности канала. Сигнал в каждой подполоске можно независимо кодировать и модулировать с синхронной скоростью передачи символов l/A/" и с оптимальным распределением мощности /(/) . Если Af очень мало, тогда С(/) по существу константа во всейПодполоске, так что выравнивание не требуется, поскольку МСИ пренебрежимо мала. Модуляция со многими несущими используется в модемах как радио-, так и телефонных каналах. Модуляция со многими несущими также предполагается для применения в будущем цифровом звуковом вещании. Особо подходящее применение для систем со многими несущими - это цифровая передача по медным проводным соединительным линиям. Типичная характеристика канального затухания для такой соединительной линии иллюстрируется на рис. 12.2.2. Мы видим, что коэффициент передачи быстро падает с ростом частоты. Такая характеристика сильно затрудняет достичь высокую скорость передачи при использовании одной несущей и эквалайзера на приеме. Ухудшение качества из-за МСИ очень велико. С другой стороны, модуляция со многими несущими с оптимальным распределением мощности обеспечивает возможность для высокой скорости передачи. Доминирующий шум при передаче по соединительным линиям это взаимная интерференция от сигналов других телефонных линий, расположенных в том же кабеле. Распределение мощности этого типа шума также зависит от частоты, что можно принять во внимание при распределении возможной передаваемой мощности. Процедура синтеза системы КАМ со многими несущими для неидеального линейного фильтрованного канала была дана Калетом (1989). В этой процедуре суммарная битовая скорость максимизируется посредством расчета оптимального деления мощности по поднесущим и оптимального выбора числа бит на символ (размера сигнального созвездия КАМ) для каждой поднесущей при учете ограничений на среднюю мощность передатчика и при условии, что вероятности ошибочного приёма символов для всех поднесуших равны. Ниже мы представим разработку модулятора КАМ со многими несущими и демодулятора, которая базируется на дискретном преобразовании Фурье (ДПФ)для генерации многих несущих. 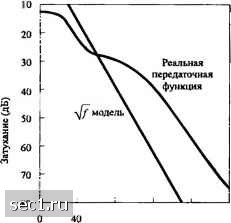 160 360 640 1000 Частота / ( кГц ) Рис12 2.2. Коэффициент передачи 24 gauge 12 ktf PIC loop [Werner ©IEEE] Разработки последних лет показывают, что системы с одной несущей вполне конкурентоспособны по сравнению с системами на многих несущих при цифровой передаче по медным проводным соединительным линиям (VDSL) с учетом реальных свойств канала (прп). 0 ... 190191192193194195196 ... 262 |