12.2.2. Система со многими поднесущими, основанная на быстром преобразовании Фурье

В этом разделе мы опишем систему связи со многими поднесущими которая использует алгоритм быстрых преобразований Фурье (БПФ) для синтеза сигнала на передаче и для демодуляции принимаемых сигналов на приеме. БПФ просто эффективный вычислительный инструмент для разработки дискретного преобразования Фурье (ДПФ).

Рис. 12.2.3 иллюстрирует блок-схему системы связи со многими несущими.

Входные да111:].е

После ю-1иП1:лы10-пар.шле-.и.пии буфер

Модуляюр

со М1101ИМИ

несущими (обратное ДПФ)

Добавление циклического

префикса, параллельно-последовательное преобразование

Цифро-аналоговое преобразована (ЦАП)

Выход -►

Вьгходныс Лан[ые

<-

Аналого-цифровое

преобразование

(АЦП)

Рис.12.2.3. Система связи со многими несущими

Буферное устройство превращает информационную последовательность в параллельно передаваемые блоки по Nj- бит. Каждый фрагмент из Л- бит делятся на N групп, причём /-Й группе назначается «, бит и

J:n,=N,. (12.2.9)

Ках<дая группа может кодироваться отдельно, так что число выходных символов кодера для / й группы > .

Удобно рассматривать модуляцию со многими несущими как модуляцию, составленную из N независимых КАМ каналов, работающих с одинаковой скоростью 1/7, но имеющих независимые КАМ созвездия, т.е. каждый / -й канал использует М = 2" сигнальных точек. Обозначим комплексные точки сигнала, соответствующие информационным символам в подканалах Х, к = 0,1, ...,N-\. Для получения

многочастотного сигнала с N поднесущими по информационным символам {х,.] воспользуемся обратным ДПФ (ОДПФ).

Однако, если мы вычислим N -точечное ОДПФ по {Х}, то получим комплексную последовательность чисел, которая не эквивалентна N КАМ-модулированным поднесущим. Вместо этого введём N = 2N информационных символов, определённых следующим образом:

Хк=Х1, k = \,...,N-l (12.2.10)

и Х,=Яе(Хц), Х =1т(Ха). Таким образом, символ Х распадается на две части.

причём обе части - вещественные. Теперь N -точечное ОДПФ порождает вещественную последовательность

1 м-1

Jlnnlc/N

1 N-l

п = 0, l,...,N-\,

(12.2.11)

где - масштабный множитель.

Последовательность {х„,0< л <jV-1} соответствует отсчётам суммы x{t) N сигналов по всем поднесущим:

<) = ::}ТХкс""\ 0<t<T, (12.2.12)

где Т- символьный интервал. Видно, что частоты поднесущих равны fi = k/T. к = 0,\,...,N. Далее дискретная во времени последовательность {х„) по (12.2.11) представляет собой отсчёты x{t), взятые в моменты времени i = nT/N, где /? = 0, 1......V-1.

Вычисление ОДПФ по {Хк}, как видно из (12.2.11), можно рассматривать как умножение каждой точки данных Хк на соответствующий вектор

vt = [ию, Uii... uv(w-i)], (12.2.13)

(12.2.14)

как показано на рис. 12.2.4. Во многих случаях вычисление ДПФ может быть эффективно выполнено с использованием алгоритма быстрого преобразования Фурье (БПФ).

Данные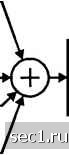

Добавление циклического префикса

В канал

Рис. 12.2.4. Синтез сигнала для модуляции со многими несущими на основе обратного ДПФ

На практике отсчёты сигнала подаются на цифро-аналоговый преобразователь СЦАП). а затем на ФНЧ, на выходе которого образуется канальный сигнал x(t).

Проходя по каналу связи, этот сигнал искажается:

r(t) = x(t)®h(t) + n(t), (12.2.15)

где h{t) - импульсная характеристика канала, ® - знак свёртки, а n(t) - помеха.

При выборе полосы частот каждого подканала А/ достаточно малой величины длительность элементарного символа T = l/Af становится большей, чем интервал

временного рассеяния канала. Точнее говоря, мы вправе предположить, что это рассеяние охватывает v + \ отсчётов сигнала, причём v«N. При этом для устранения явления МСИ можно использовать защитный интервал длительностью vT/N , вводимый между смежными сигнальными блоками.

Другой метод борьбы с МСИ состоит в присоединении циклически повторяемого префикса между блоками, состоящими из N отсчётов сигнала {xg,x,,...,.Tf ,}. Этот

префикс состоит из отсчётов х „, >jv „+i, •••, присоединяются к началу каждого блока. Таким образом, длина каждого блока увеличивается до jV + v отсчётов, и их теперь можно индексировать величинами н = v,1, причём первые v отсчётов образуют префикс. Тогда, если (/7„,0<;/<v} означают отсчёты импульсной характеристики канала, то их свертка с {x,~v < п < N-l} даёт {/;,}-принимаемую последовательность Нас интересуют лишь отсчёты для О < п < N - \, по которым можно восстановить

переданную информационную последовательность, используя для демодуляции yV-точечное ДПФ. Следовательно, первые v отсчётов отбрасываются за

ненадобностью.

С частотной точки зрения, если дана импульсная характеристика канала ( ,„ О < < г}, то коэффициент передачи для -й поднесущей равен

Jhe--"". (12.2.16)

Благодаря префиксу смежные сигнальные блоки не интерферируют и, следовательно, демодулированная последовательность может быть представлена в виде

Х,--Н,Х, + ц„ k = 0,],...,N-\, (122.17)

где {Х\ ]- выход демодулятора, т.е. N - точечного ДПФ , а г),. - ошибка.

обусловленная аддитивным шумом. Заметим, что, выбирая N»v, можно потерю скорости, вызванную префиксными вставками, сделать пренебрежимо малой.

Как показано на рис. 12.2.3, сигнал демодулируется путём вычисления ДПФ после аналого-цифрового преобразования. При этом ДПФ может рассматриваться как

перемножение отсчётов принятого сигнала {/;} с \1, где v„ определено в (12.2.13). Как и

в случае с модулятором, вычисление ДПФ может быть эффективно выполнено с использованием алгоритма быстрого преобразования Фурье (БПФ).

При необходимости несложно оценить и скомпенсировать канальный множитель {Ht\

перед тем, как передать Х в детектор и декодер. Для этого может быть использован

«обучаюший» сигнал либо в виде известной модулирующей последовательности на каждой поднесущей, либо в виде немодулированной несущей. Если параметры канала изменяются во времени медленно, то можно отследить их изменения во времени с использованием решений с выхода детектора или даже декодера. Таким образом, система передачи со многими поднесущими может быть сделана адаптивной.

Многочастотная КАМ, описанная выше, может быть использована во многих практических приложениях, в том числе в высокоскоростной передаче данных по телефонным линиям.

При выборе способа реализации ДПФ необходимо иметь в виду, что с точки зрения вычислительной сложности при N <32 выгоднее использовать обычное ДПФ, а при N>32- БПФ, причём выигрыш быстро растёт с увеличением N .

Есть одно ограничение на использование ДПФ в модуляторах и демодуляторах, обусловленное относительно большими боковыми лепестками частотной характеристики, присущими фильтрам ДПФ-типа. Первый лепесток лишь на 13 дБ ниже основного максимума, соответствующего выбранной поднесущей. Поэтому все приложения, основанные на использовании банков ДПФ-фильтров, уязвимы по отношению к межканальной интерференции (МКИ). Если вследствие канальных аномалий МКИ является проблемой, то следует использовать другие банки цифровых фильтров, которые