которое определяет число чипов на информационный символ. Это значит, что это

число фазовых сдвигов, которые возникают в переданном сигнале на символьном интервале Tf,=\lR. Рис. 13.2.1(a) иллюстрирует взаимосвязь между ПШ сигналом и

сигналом данных.

Предположим, что кодер берет каждый раз на временном интервале кТ к информационных символов и генерирует двоичный линейный блоковый код.

Интервал времени, выделенный для передачи элементов кода, равен kl с, число чипов на этом временном интервале равно kL. Мы можем выбрать длину блока кода п = kL, тогда скорость кода к/п. Если кодер генерирует двоичный свёрточный код со скоростью к/п, число чипов на временном интервале кТ, также равно n = kL.. Значит,

нижеследующее обсуждение применимо как к блоковым, так и к свёрточным кодам.

Один метод для включения ПШ последовательности в передаваемый сигнал сводится к непосредственному изменению кодовых символов их суммированием по mod 2 с ПШ последовательностью.

Если используется четырёхфазная ФМ, то одна ПШ последовательность суммируется с информационной последовательностью и передается синфазной несущей, а вторая ПШ последовательность суммируется с другой информационной последовательностью и передается квадратурной несущей. Во многих широкополосных системах одна и та же двоичная информационная последовательность суммируется с двумя ПШ последовательностями для формирования двух квадратурных компонент. Таким образом, генерируется сигнал четырёхфазной ФМ с двоичным информационным потоком.

Итак, каждый информационный символ изменяется путём его суммирования с символом ПШ последовательности. Если Ь\ представляет /-й символ ПШ последовательности, а с, - соответствующий символ на входе кодера, то сумма по mod 2 даёт

a,h,®c,. (13.2.3)

Таким образом, а, = 1 если А, = 1 и с, = О или А, = О и с, = 1; также я, = О когда А, = 1 и с = 1 или когда 6, = О и с, = О. Мы можем сказать, что д, = О, когда h. = с, и а, = 1, когда h. Ф с . Последовательность {я,} отображается в двоичный ФМ сигнал в виде согласно правилу:

5(/) = ±Re[(/)"

\-g{t-}TX («, = 0,

где gif) представляет импульс длительностью 1\ с произвольной огибающей.

Суммирование по mod 2 кодовой последовательности {с,} и последовательности {Л,}

ПШ генератора можно также представить как умножение двух сигналов. Чтобы продемонстрировать эту точку зрения, предположим, что элементы кодовой последовательности отображаются в двоичный ФМ сигнал согласно отношению

c,(0 = (2c,-l)(/-/TJ. (13.2.5)

Аналогично определяем сигнал /;,(/) так

р,(0 = (2б,-1)М/-Т), (13.2 6)

где /?(/) - прямоугольный импульс длительности . Тогда эквивалентный низкочастотный передаваемый сигнал, соответствующий, /-му кодовому символу равен

gM) = P.iOc.iO = (2b, -l)(2c, -l)g(/-/7;). (13.2.7)

Этот сигнал идентичен тому, который определяется (13.2.4) и который получен от последовательности \сг,У Следовательно, суммирование по mod 2 кодовых символов сТТШ последовательностью ведет к отображению в ФМ сигнале, который эквивалентен умножению двоичного ФМ сигнала, генерированного кодовыми символами, с последовательностью прямоугольных символов единичной амплитуды, каждый длительностью 7, и полярностью, которая определяется ПШ последовательностью

согласно (13.2.6). Хотя легче реализовать суммирование по mod 2 и затем ФМ вместо умножения сигналов, удобно для целей демодуляции рассматривать сигнал в мультипликативной форме, определяемой (13.2.7). Функциональная блок-схема четырёхфазовой ФМ с 1111 широкополосным сигналом показан на рис. 13.2.1(b).

Принимаемый эквивалентный низкочастотный сигнал для /-го кодового элемента определяется так:

r,{l)= (2b, -1)(2с,-\)g(t-iT) + zO), (13.2.8)

где z{t) представляет сигнал интерференции или глушения, который искажает информацию в полезном сигнале. Интерференция считается стационарным случайным процессом с нулевым средним.

Если z{f) является отсчетной функцией комплексного гауссовского процесса, оптимальный демодулятор можно реализовать или как фильтр, согласованный с сигналом g{f), или как коррелятор, как показано на блок-схемах рис. 13.2.2. При реализации согласованным фильтром выход согласованного фильтра умножается на величины (2Ь, -1), которые получаются от генератора ПШ на приёме, когда он правильно

синхронизирован. Поскольку (26, -1) = 1, когда Ь, =0 и Z>, = 1, то влияние ПШ

последовательности на принимаемый кодовый символ устраняется.

На рис. 13.2.2 мы также видим, что взаимная корреляция может быть выполнена одним из двух путей. Первый, иллюстрируемый на рис. 13.2.2(b), выполняет предварительное умножение г.(0 на сигнал />,(/), генерируемый ПШ генератором, а затем осуществляется

взаимная корреляция с g*{f) и стробирование выхода на интервале каждого чипа. Второй метод, иллюстрированный на рис. 13.2.2(c), включает сначала взаимную корреляцию принимаемого сигнала с g*{i), стробирование выхода коррелятора и затем умножение этого выхода на (26, -1), которое получается из ПШ генератора.

Если z{t) не является гауссовским случайным процессом, методы демодуляции, иллюстрируемые на рис. 13.2.2, не являются больше оптимальными, тем не менее, мы можем всё же использовать любую из этих трех структур демодулятора для демодуляции принимаемого сигнала. Если статистические характеристики интерференции z{t) неизвестны априори, это, конечно, один из возможных подходов. Альтернативный метод, который описывается ниже, использует адаптивный фильтр до согласованного фильтра или коррелятора для подавления узкополосной интерференции. Целесообразность этого второго метода также излагается ниже.

Для простоты мы считаем, что канальное ослабление а = 1, а фазовый сдвиг в канале нулевой. Поскольку предполагается когерентное детектирование ФМ сигнала, то произвольный фазовый сдвиг в кана.1е компенсируется до демоду.чятора.

Генератор микротактов

у 26,-1

декодеру

Генератор ПШ сигнала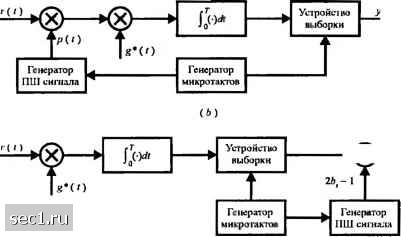

К декодеру

ЮО » к декодеру

(< )

Рис. 13.2 2. Возможные структуры демод>ляторов для псевдошумовы.\ (ПШ) широкополосных сигналов

В разделе 13.2.2 мы определим вероятность ошибки для широкополосной системы с ПП (с рассеянным спектром) в присутствии широкополосной и узкополосной интерференции. Расчет базируется на предположении, что демодулятор имеет одну из трёх эквивалентных структур, показанных на рис. 13.2.2.

13.2.1. Качество декодера

Обозначим неквантованный выход демодулятора через y/j, \<j<n. Сначала

рассмотрим линейный двоичный (п,к) блоковый код и, без потери общности, предположим, что передается кодовое слово из одних нулей.

Декодер, который выполняет детектирование мягких решений, вычисляет корреляционные метрики

СМ, = X(2S-)yj = 1 2, 2* , (13.2.9)

где с, означает j-й символ в i-м кодовом слове. Корреляционная метрика, соответствующая кодовому слову из одних нулей, равна

CM,=2n+f(2c,-\)i2bj-\)v =

(13.2.10)

= 2«g,-S(2-l)v,

где Vj, \< j <n - аддитивное шумовое слагаемые, которые искажает j-ii кодовый символ, а f - энергия чипа. Величина определяется так: