v. = Re

7 = 1. 2, ....«.(13.2.11)

Аналогично, корреляционная метрика, соответствующая кодовому слову с, с весом , равна

( 2w \ Ш=2,« 1---

V. п )

+Z(2»v-J)(4-lh. (13.2.12)

Следуя примеру, использованной в разделе 8.1.4, мы можем определить вероятность того, что СМ > СМ. Разница между СМ, и СМ„ равна

D = CM,-CM„=4%w„-2±c,i2b.-l)v. (13.2.13)

Поскольку кодовое слово с„ имеет вес w, имеется ненулевых компонент при

суммировании шумовых слагаемых в (13.2.13). Мы можем предположить, что минимальное расстояние кода достаточно велико, так что мы можем обратиться к центральной предельной теореме при суммировании шумовых компонент. Это предположение имеет силу для широкополосного сигнала ПШ, который имеет показатель расширения спектра 20 или больше. Таким образом, сумма шумовых компонент моделируется гауссовской случайной величиной. Поскольку £(2А-1) = 0 и £(v) = 0,

среднее для второго слагаемого в (13.2.13) также равно нулю. Его дисперсия

(13.2.14)

7-1 1-1

Последовательность двоичных символов ПШ предполагается некоррелированной. Следовательно,

426,-lX2A,-l)]=5, (13.2.15)

<«=4h„£(v). (13.2.16)

где E(v) - второй момент любого элемента {v}. Этот момент легко вычислить:

E(v) = ]]g(Og{x) it - x)dtdx = ]piffMW, (13.2.17)

где Ф„(т) = I£[2*(/)2(/+t) -автокорреляционная функция, a Ф„(/) - спектральная плотность мощности интерференции z{t).

Мы видим, что если интерференция имеет одинаковую спектральную плотность внутри полосы частот переданного сигнала, т.е.

Ф(/) = Л. \f\\W, (13.2.18)

тогда второй момент в (13.2.17) E{v) = 2%Jq и, следовательно, дисперсия интерференционного слагаемого в (13.2.16) равна

<=4Jo.- (13.2.19)

В этом случае вероятность того, что D<0 равна

Типичный показатель расширения спектра для широкополосных сигналов имеет порадрк 100 и больше. Если полоса полосового канала w, то полоса эквивалентного низкочастотного канала \ w.

w

(13.2 20)

Но энергия на кодовый символ можно выразить через энергию информационного

символа (

Представив это в (13.2.20), получаем

(13.2.21)

(13.2 22)

где =4/Л~ ОСШ на информационный бит. Наконец, вероятность ошибки кодового

слова можно оценить сверху границей

(13.2.23)

где -2* Заметим, что это выражение идентично вероятности ошибки кодового слова при декодировании мягких решений линейного двоичного блокового кода в канале с АБГШ

Хотя выше мы рассмотрели двоичный блоковый код описанная процедура аналогична и для Ui,k) свёрточного кода.

Результат такого рассмотрения дает следующую верхнюю границу для эквивалентной вероятности ошибки на бит

(13.2.24)

Набор коэффициентов {Pj} получается из расширения производных передаточной функции T{1),N), как описано в разделе (8 2.3).

Далее мы рассмотрим узкополосную интерференцию, концентрированную около несушей (около нуля для эквивалентного низкочастотного сигнала). Мы можем фиксировать суммарную (среднюю) мощность помехи -f-JJiV, где ./.-величина

спектральной плотности мощности эквивалентной широкополосной интерференции (сигнал глушения). Узкополосная интерференция характеризуется спектральной плотностью мощности

ф..(/) =

(1/1 >.)-

(13.2.25)

где W » W,

Подстановка (13.2.25) для Ф,,(/) в (13.2.17) дает

W

GUYJf.

(13.2.26)

Величина £"(v") зависит от спектральных характеристик g(t). В следующем примере мы рассмотрим два специальных случая.

Пример 13.2.1. Предположим, что g(t) - прямоугольный импульс, показанный на рис. 13.2.3(a), а G(/)- соответствующая спектральная плотность энергии, показанная на рис. 13.2.3(b).

«(О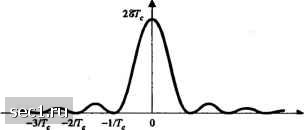

1/Т, 2/Г, З/Г, /

(а) (Ь)

Рис. 13.2.3. Прямоугольный имщльс и его энергетический спектр

Для узкополосной интерференции, определяемой (13.2.26), дисперсия общей интерференции равна

sin 7

2 ..ч 8wjyY

-0/2

a5c, (13.2.27)

где P = JKr. Рисунок 13.2.4 иллюстрирует величину этого интеграла для О < Р < 1.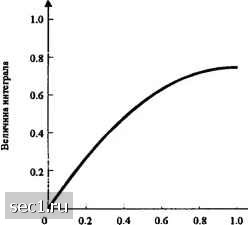

Рис. 13.2.4. График зависимости величины интеграла в (13.2.7) от интервала интефирования р

Мы видим, что величина интеграла имеет верхнюю границу, WJ. Следовательно,

В пределе, когда становится нулём, интерференция определяется импульсом на несущей. В этом случае интерференция представляет чисто гармонический сигнал и она обычно называется гармонической помехой на несущей (ГПН, CW jamming signal). Спектральная плотность мощности равна

Ф„(/) = 5(/), (13.2.28)

и соответствующая дисперсия для величины I) = СМ -СМ„ равна