а;„=4„Лрс(о)Г=8?:„,7:.л,,.

Вероятность ошибки кодового слова для ГПН имеет верхнюю границу

(13.2.29)

(13.2.30)

Но f=Ry, Далее и .JJW = .J„. Следовательно, (13.2.30) можно выразить

так:

(13.2.31)

что является результатом, полученным раньше для широкополосной интерференции. Это г результат говорит о том, что ГПН имеет то же влияние на качество, что и эквивалентньи"! широкополосный мешающий сигнал. Эта эквивалентность обсуждается ниже.

Пример 13.2.2. Определим качество широкополосной системы с ПП в присутствии CW jammer со средней мощностью .У,, когда импульс переданного сигнала

определяется полупериодом синусоиды, как показано на рис. 13.2.5, т.е.

/ \ 4. . я/ >(0 = Jy"sm-, 0<(<f.

(13 2.32)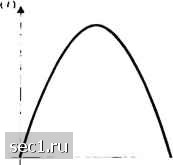

о- 7;

Рис. 13.2.5. CiiHVCoiun.ibHbiii сигна.1ьный импульс

Дисперсия интерференции для такого символа

64...

а;=4и„,/„!ОД-7:./,.и,..

Таким образом, верхняя граница вероятности ошибки кодового слова

(13 2 33)

(13.2.34)

Мы видим, что качество, получаемое таким импульсом на 0,9 дБ лучше, чем то, которое получено при прямоугольном импульсе. Напомним, что такая огибающая, используемая в офсетной КФМ, ведёт к сигналу ММС. ММС модуляция часто используется в широкополосных системах с ПП.

Выигрыш обработки и помехозащищённость (jamming margin). Интересная интерпретация характеристики качества широкополосного сигнала с ПП можно получить, выражая энергию сигнала на бит через среднюю мощность. Это значит, что i; 1,,Т„,

где Рр-средняя мощность сигнала и 7-символьный интервал. Рассмотрим качество,

полученное в присутствии CW-jamming для прямоугольного импульса, обсуждённого в примере 13.2.1. Если подставить значения для и 7 в (13.2.31), мы получим

ср-с

(13.2.35)

где Z-число чипов на информационный символ, а ./ - отношение мощности

сигнала к мощности помехи.

Аналогичный результат получен для широкополосного мешающего сигнала, для которого качество даётся (13.2.23). Для энергии сигнала на бит имеем

%=PJb=, (13.2.36)

где R - информационная скорость в бит/с. Спектральная плотность мощности для мешающего сигнала можно выразить так:

J,=JJW. (13.2.37)

Используя отношения (13.2.36) и (13.2.37), отношение %,IJa можно выразить так

Ц. -ср/ WIR

J.I Р.

(13.2.38)

Отношение Jp/P-это отношение средней мощности помехи к средней мощности сигнала, которое обычно больше единицы. Отношение W/R = T/T=B=L как раз

показатель расширения полосы частот или, что эквивалентно, число чипов на информационный бит. Это отношение обычно называется выигрышем обработки (ВО) широкополосной системы с ПП. Оно представляет преимущество, выигранное относительно помехи, которое получается благодаря расширению полосы частот передаваемого сигнала. Если будем интерпретировать /Jq как ОСШ, требуемое для достижения заданной вероятности ошибки, а W/R как допустимый показатель расширения полосы частот, соотношение JIP будет иметь смысл помехозащищённости (запаса по

помехе) широкополосной системы с ПП. Другими словами, помехозащищённость - это наибольшая величина, которую может принять отношение JfPp, при котором система

передачи ещё удовлетворяет заданной вероятности ошибки.

Качество декодера мягких решений для линейного двоичного кода {п,к), выраженное через выигрыш обработки и помехозащищённость, определяется так:

2W/R „

XPJp.

PmIQ

<{M-\)Q

(13.2.39)

В дополнение к зависимости от выигрыша обработки W/R и JIP мы видим, что качество зависит от третьего множителя, именно R. Этот множитель определяет выигрыш кода. Нижняя граница этого множителя равна Rd. Таким образом, помехозащищённость, достигаемая широкополосными сигналами с ПП, зависит от выигрыша обработки и выигрыша кодирования.

Некодированные широкополосные сигналы с ПП. Результаты качества, данные выше для широкополосных сигналов с ПП, генерируемые посредством {п,к) кода, могут быть конкретизированы для тривиального кода, именно для двоичного кода с

повторением. В этом случае А: = 1, а вес ненулевого кодового слова \v = n. Таким образом, Rjv = 1, следовательно, качество двоичной системы сигналов определяется так

Р,=0

2W/R

ср ср у

(13.2.40)

Заметим, что тривиальный код не дает выигрыш кодирования. Он даёт выигрыш обработки WIR .

Пример 13.2.3. Предположим, что мы желаем достичь вероятность ошибки 10"* или меньше при помощи широкополосной системы с ПП. Желательный показатель расширения полосы WIR = \QOO. Определим помехозащищённость.

Требуемая величина %,IJq для достижения вероятности ошибки на бит 10"* при

помощи некодированной двоичной ФМ равна 10,5 дБ. Выигрыш обработки равен 101gl000 = 30дБ. Следовательно, максимальное допустимое значение отношения мощностей помехи и сигнала, т.е. помехозащищённость, равно

10lg = 30-10,5 = 19,5дБ.

Поскольку эта помехозащищённость достигается для некодированной широкополосной системы с ПП, её можно увеличить путём кодирования информационной последовательности.

Имеется другой путь для рассмотрения процессов модуляции и демодуляции для некодированной (код с повторением) широкополосной системы с ПП. У модулятора сигнал, генерируемый кодом с повторением, например при прямоугольном импульсе, идентичен прямоугольному импульсу .v(/) с единичной амплитудой длительностью 1\ или его обратному значению, в зависимости от того является ли информационный символ соответственно 1 или 0. Это видно из (13.2.7), где кодовые чипы {с;} внутри

информационного символа равны 1 или 0. ГШ! последовательность умножается на s{f) или -s{f). Так, если информационный символ 1, то чипов, генерируемых ПШ

генератором передаются с той же полярностью. С другой стороны, если информационный символ О, то L чипов при умножении на меняют полярность.

Демодулятор для кода с повторением, реализованный как коррелятор, иллюстрируется на рис. 13.2.6.

г{1)

Генератор ПШ иоследовагел!.-иосги

Гс пера юр микритактон

Тактив1.1Й генератор

Рис. 13.2.6. Демодулятор корреляционного типа для кода с повторением

Видим, что интервал интегрирования в интеграторе равен символьному интервалу 7J,.

Таким образом, декодер для кода с повторением ограничен и его функция реализуется демодулятором.