Тогда максимальное число пользователей, которое может содержать CDMA система, равно

K=Kd-l- (13.2.60)

Если W/R = 100 и Rcd=4, как это было получено кодом Голея (24,12), то максимальное число 7*/„=21. Если W/R = \000 и Ж/Л = 1000, это число получится равным =201.

При определении максимального числа одновременных пользователей канала мы безоговорочно предположили, что ПШ кодовые последовательности взаимно ортогональны и интерференция от других пользователей суммируется только по мощности. Однако, ортогональность среди определенного числа ПШ кодовых последовательностей не легко достичь, особенно если требуемое число ПШ кодовых последовательностей велико. Действительно, выбор хорошего ансамбля ПШ последовательностей для системы CDMA - важная проблема, которая привлекла значительное внимание в технической литературе. Мы хотим обсудить эту проблему в разделе 13.2.3.

13.2.3. Влияние импульсной интерференции на широкополосные ПП системы

До сих пор мы рассмотрели влияние непрерывной интерференции или непрерывной прицельной помехи на широкополосные ПП сигналы. Мы видели, что выигрыш обработки и выигрыш кодирования обеспечивают средство для преодоления вредных влияний этих видов интерференции. Однако существует мешающий сигнал, который имеет весьма существенное влияние на качество широкополосных ПП систем. Такой мешающий сигнал состоит из импульсов с равномерным частотным спектром, который покрывает полностью полосу частот сигнала W. Их обычно называют импульсной интерференцией или парциально-временным мешающим сигналом (ПВМС).

Предположим, что мешающий сигнал имеет среднюю мощность в полосе частот

сигнала fV. Тогда Jq=JIW . Вместо непрерывной передачи источник мешающего

сигнала передаёт импульсы повышенной мощности J/ct за долю времени а, т.е.

вероятность, того, что источник мешающего сигнала создаёт в данный момент времени помеху, равна а. Для простоты мы предположим, что импульсы интерференции простираются на целое число сигнальных интервалов и таким образом влияют на целое число символов. Если источник мешающего сигнала не выдаёт помеху, то переданный сигнальный бит предполагается принятым без ошибки, а когда он работает, вероятность

ошибки для некодированной широкополосной ПП системы равна о{2аЦ,/Jq). Таким

образом, средняя вероятность ошибки на бит равна

PAoL) = oLQ{j2a%/J,)=aQ

l2aW/R

(13.2.61)

Источник мешающего сигнала выбирает параметр а (называемый иногда дежур1ым циклом-duty cycle), чтобы максимизировать вероятность ошибки. Дифференцируя (13.2.61) по а, находим, что наихудший случай ПВМС имеет место, когда

• (/Л 0,71)

%.IJo . (13.2.62)

1, (/Л<0,71)

а соответствующая вероятность ошибки равна

0,083 0,083.

1WIR

,/./„> 0.71)

(г/.Л,<о.71)

(13.2.63)

Вероятность ошибки, определяемая (13.2.61) для а =1,0, 0,1 и 0,01, а также в наихудшем случае а* даны на рис. 13.2.8. Сравнивая вероятность ошибки при мешающем непрерывном гауссовском шуме (а=1) и наихудшем случае ПВМС, видим большую разницу в качестве, которая примерно равна 40 дБ при вероятности ошибки 10.

10-0

Худший случ.й импульсного мешающего сигнала (ct - а*)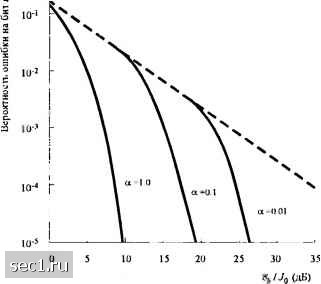

Рис. 13.2.8. Характеристики псевдошумовой двоичной ФМ с импульсным меш<1ющим сигналом

Мы хотим подчеркнуть, что проведенный анализ приложим, когда длительность мешающего импульса равна или больше длительности символа. Дополнительно мы хотим указать, что практические соображения могут запретить источнику мешающего сигнала достигать больших пиковых значений мощности (малых значений а). Всё же, вероятность ошибки, даваемая (13.2.63), служит верхней границей для качества некодированной двоичной ФМ в наихудшем случае ПВМС. Ясно, что качество широкополосной ПП системы при наличии такой помехи наиболее низкое.

Если мы просто прибавим кодирование к широкополосной ПП системе, улучшение относительно некодированной системы равно выигрышу кодирования. Таким образом, требуемое <4/./„ уменьшится за счет выигрыша кодирования, который в большинстве

случаев ограничен величиной меньшей 10 дБ. Причина плохого качества заключается в том, что длительность импульса мешающего сигнала можно так выбрать, чтобы влиять на многие соседние кодовые символы, когда источник помехи включён. Следовательно,

Это означает, что источник мешаюшсго сигнала при использовании оптимальной стратегии может добиться своей цели, расходуя мощность на 40 дБ меньше (прп).

вероятность ошибки кодового слова велика из-за импульсного характера мешающего сигнала.

Чтобы улучшить качество, мы можем перемежать кодовые символы до их передачи по каналу. Влияние перемежения, как говорилось в разделе 8.1.9, сводится к тому, чтобы сделать кодовые символы, поражённые глушителем, независимыми.

Блок-схема цифровой системы связи, которая включает перемежение-деперемежение, показана на рис. 13.2.9. Показана также возможность того, что приёмник знает состояние источника помехи, т.е. знает, включен он или нет.

Дапше

Кодер

Перемежитель

Данные А-

Состояние источника помехи

Декодер

Декодер

Модучятор

ПШ генератор

ПШ генератор

Демодулятор

Канал

Рис. 13.2.9. Блокч:хема АП системы связи

Знание состояния источника помехи (называемое сторонней информацией) иногда имеется в распоряжении при измерении уровней шума в канале в соседних частотных полосах. В нашей трактовке мы рассмотрим два экстремальных случая, именно, нет никакой информации о состоянии источника помехи или имеется полное знание о его состоянии. В любом случае, случайная величина С,, представляющая состояние источника

помехи, характеризуется вероятностями

Р(С = 1) = а, Р(С = 0) = 1-а. Когда источник помехи включён, канал моделируется как имеющий АБГШ со спектральной плотностью мощности NJ/aJ/aW, а когда источник помехи

выключен - в канале нет шума. Знание состояния источника помехи подразумевает, что декодер знает, когда = 1 и когда С, = 0, и используют эту информацию при вычислении корреляционных метрик. Для примера, декодер может взвешивать выход демодулятора для каждого кодового символа величиной обратной уровня мощности шума на данном интервале. Альтернативно декодер может дать нулевой вес для пораженного помехой символа.

Сначала рассмотрим влияние помехи без знания состояния источника помехи. Предполагается, что пара перемежитель-денеремежитель приводит к независимым попаданиям помехи на кодовые символы. Как пример качества, достигаемого кодированием, мы приводим результат качества из статьи Мартина и Мак-Адама (1980). Здесь качество двоичных свёрточных кодов вычислена для наихудшего случая ПВМС. Рассматривается декодирование Витерби жестких и мягких решений. Мягкие решения получены квантованием выхода демодулятора на восемь уровней. Для этой цели используется равномерный квантователь для которого пороговые уровни оптимизированы применительно к уровням импульсного шума глушителя. Квантователь играет важную