роль для ограничения размера выходов демодулятора, когда источник помехи включен. Эффект ограничения гарантирует, что любой «удар» на кодовый символ не будет существенно влиять на соответствующие метрики пути.

Оптимальный «дежурный цикл» для ПВМС в кодированной системе обычно обратно пропорционален ОСШ, но его величина отличается от той, которая определяется (13.2.62) для некодированной системы. Рис.13.2.10 иллюстрирует графически оптимальный дежурный цикл глушителя при декодировании жёстких и мягких решений для свёрточного кода со скоростью 1/2. Соответствующие результаты для вероятности ошибки для этого наихудшего случая ПВМС иллюстрируются рис. 13.2.11 и 13.2.12 для скорости кода 1/2 и кодового ограничения Ъ<К<9, соответственно при декодировании жёстких и мягких решений АВ.

1 .г

I i

5 10-:

1(1

ПВМС

/(Duiriiiai ФМ

Жсс1К1к решети

MaiKiic решснна юиьслинешии ipjiiiiua)

1(1 15 Е,/7„ (JD)

ООЬСД1К.1Я IIMIUIUJ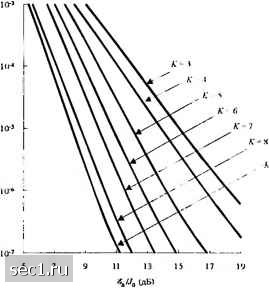

20 25 311 Рис. 13.2 II. .\»рактерисгнки сиёрточпого кчгда соскиросгыо 1/2

с л<ки.1срим жбстких рсшсмнн 13 1срГ>и, лштчмпи ФМ с оптимальным ПВМС

Рис. 13.2 10. OirKLMujiMiLiH дежурный Ш1кплля ПВМС

[Шпт и Л/сЛс/чот (1980), О 19X0 IEEE \

Для примера заметим, что при Я, =10" свёрточный код с К=1 при декодировании МЯГКИХ решений требует -7,6 в то время декодирование жёстких решений требует

(•t,/./„ = 11,7дБ. Эта разница в 4,1 дБ в ОСШ относительно велика. При непрерывном

гауссовском шуме соответствующие ОСШ для вероятности ошибки 10"" равна 5 дБ для декодирования мягких решений и 7 дБ для декодирования жестких решений. Таким образом, случай наихудшего ПВМС уменьшает качество на 2,6 дБ для декодирования мягких решений и на 4,7 дБ для декодирования жестких решений. Эти уровни деградации увеличиваются по мере уменьшения кодового ограничения. Важнейшее обстоятельство, однако, то, что потери в ОСШ, обусловленные помехой, уменьшаются от 40 дБ для некодированной системы до менее чем 5 дБ для кодированной системы при использовании свёрточного кода с К=7 и скорости 1/2.

Простой метод для вычисления качества (кодированной) системы в условиях действия ПВМС сводится к вычислению параметра предельной скорости как предложено Омурой и Левитом (1982). Например, для двоичной кодовой модуляции предельную скорость можно выразить так

/<, = l-log(l + Z)J, (13.2.64)

Объединенная rpauuii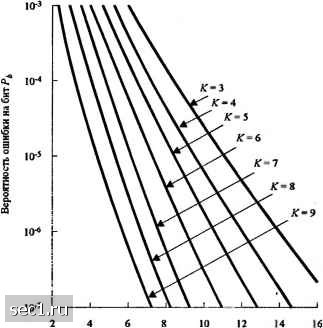

blJo (дБ)

Рис. 13.2.12. Характеристики сверточного кода со скоростыо 1/2 с декодером мягких решений Витерби, двоичной ФМ с оптимальным ПВМС [MartinuMcAdani (1980). © 1980/ЕЕ:£]

где зависит от шумовых характеристик канала и обработки декодером. Напомним, что для двоичной ФМ в канале с АБГШ и декодировании мягких решений

D„=e-"». (13.2.65)

где -энергия на кодовый символ. При декодировании жестких решений

П=4Лр(\-р) (13.2.66)

гдер - вероятность ошибочного приема кодового символа. Здесь мы имеем NsJ.

Для кодированной двоичной ФМ при импульсной помехе Омура и Левит (1982) показали, что

D„=ae-"*"»

для декодировании мягких решений при знании состояния глушителя,

!шений при знании состояния глушителя, „ = min {а ехр(А?8?Ло / а)+1 - а]ехр(- 2XiS)}

для декодирования мягких решений при незнании состояния глушителя,

£>а=л/4р(1-р)

для декодировании жестких решений при знании состояния глушителя,

D„ = V4a/7(l-ap)

для декодирования жестких решений при знании состояния глушителя, где вероятность ошибки декодирования жёстких решений для двоичной ФМ равна

(13.2.67) (13.2.68)

(13.2.69) (13.2.70)

Графики Rq, как функции от %1.М, иллюстрируются на рис. 13.2.13 для случаев, оговоренных выше. Заметим, что эти графики представляют предельно-достижимую

скорость для наихудшей величины а = а*, которая максимизирует (минимизирует при каждом значении %INq. Далее заметим, что при декодировании мягких решений и отсутствии знаний о состоянии глушителя liQ. Такая ситуация возникает потому, что выход демодулятора не квантован.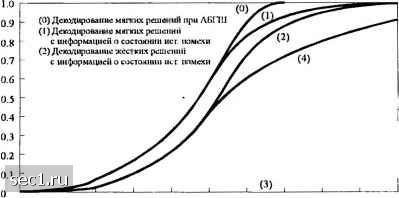

(3) Декодирование мягких решений

без информации о состоянии ист ничсхп

(4) Дешлпромнпс жёстки.х решений

без информ.ии1И о состпинии ист номсчи

-20 -16

Рис. 13.2.13. Прсдсаьиая скорость для ПП двоичной ФМ [Отит и Levitt {Ш2), © 1982 ШЕИ\

Графики рис. 13.2.13 можно использовать для расчета качества кодированных систем. Чтобы продемонстрировать процедуру, предположим, что мы желаем определить требуемое ОСШ для достижения вероятности ошибки 10" с кодированной двоичной ФМ при наихудшем случае импульсного глушения. Для конкретности предположим, что мы имеем свёрточный код с К=7 и скоростью кода 1/2. Начинаем с расчёта качества свёрточного кода с К=7, скоростью 1/2 при декодировании мягких решений в канале с АБГШ. При Я, -10"* требуемое ОСШ находим из рис. 8.2.21.

Поскольку скорость кода равна \, имеем

,/Л„=2дБ.

Теперь переходим к графикам рис. 13.2.13 и находим, что для канала с АБГШ (классический канал) с Й/Ла=2дБ соответствуюшая величина предельной скорости равна

= 0,74 бит/символ.

Если мы имеем другой канал с другими характеристиками шума (наихудший случай канала с импульсным шумом), но с той же величиной предельной скорости R„, тогда

верхняя граница вероятности ошибки на бит та же, т.е. 10 в нашем случае. Следовательно, мы можем использовать эту скорость для определения ОСШ, требуемого для случая канала с наихудшим импульсным глушением. Из графика рис. 13.2.13 находим: 10 дБ для декодирования жёстких решений при отсутствии знания о

состоянии источника помехи. 5 дБ для декодирования жёстких решений при наличии знаний о

состоянии источника помехи. 3 дБ для декодирования мягких решений при наличии знания о состоянии источника помехи.