Следовательно, соответствующие значения %,IJq для сверточного кода с К = 1 и скоростью /2 равно 13,8 и 6 дБ, соответственно.

Этот общий подход можно использовать для создания графиков вероятности ошибки для кодированных двоичных сигналов в случае канала с наихудшим ПВМС путём использования соответствующих графиков вероятности ошибки для канала с АБГШ. Подход, который мы описали выше, легко обобщить наЛ/-позиционную систему сигналов, как указано Омурой и Левитом (1982).

Сравнивая предельную скорость для кодированной широкополосной системы с ПП при двоичной ФМ, показанную на рис. 13.2.13, мы видим, что для скоростей ниже 0,7 нет ухудшения в ОСШ при декодировании мягких решений и при знании состояния источника помехи по сравнению с качеством канала с АБГШ (а = l). С другой стороны, при = 0,7

имеется разница в качестве на 6 дБ для ОСШ в канале с АБГШ и требуемый для декодирования жестких решений при отсутствии информации о состоянии источника помехи. При скоростях ниже 0,4 нет потерь в ОСШ при декодировании с жёстким решением при неизвестном состоянии источника помехи. Однако имеются и ожидаемые потери на 2 дБ при декодировании жестких решений по сравнению декодированием мягких решений в канале с АБГШ.

13.2.4. Генерирование ПШ последовательностей

Генерирование ПШ последовательностей для применения широкополосных сигналов является темой, которая привлекла особое внимание в технической литературе. Мы вкратце обсудим конструкцию некоторых ПШ последовательностей и представим важные свойства автокорреляционной и взаимокорреляционной функций таких последовательностей. Для исчерпывающей трактовки этого вопроса интересующемуся читателю рекомендуется книга Голомба (1967).

Пожалуй, наиболее широко известными двоичными ПШ последовательностями являются последовательности максимальной длины сдвигового регистра, введенные в разделы 8.1.3 в контексте кодирования, и которые снова предлагались для использования как низкоскоростные коды. Последовательность максимальной длины сдвигового регистра, или w-последовательность для краткости, имеет длину« = 2"-1 символов и генерируется т ячеечным регистром сдвига с линейной обратной связью, как иллюстрирует рис. 13.2.14. Последовательность периодическая с периодом п. Каждый период последовательности содержит 2"" единиц и 2*" -1 нулей.

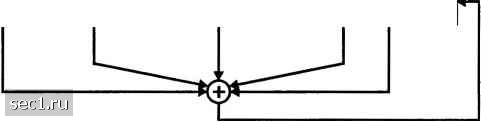Рис. 13.2.14. Схема т-каскадного регистра сдвига с .1инейной обратной связью

Для применения в качестве широкополосных ПП сигналов двоичная последовательность с элементами {0,1} отображается соответствующей последовательностью из положительных и отрицательных импульсов согласно соотношению

р,(/) = (2Л,-1)/;(/-/7), где рХО - импульс, соответствующий элементу 6, в последовательности с элементами {о,l}. Эквивалентно, мы можем сказать, что двоичная последовательность с элементами {0,1} обращается в соответствующую двоичную последовательность с элементами { Мы будем называть эквивалентную последовательность с элементами { 1,1} бшю.чярпой пос:1е<)оаате.чьиосп1ью, поскольку она определяется импульсами с положительными и отрицательными амплитудами.

Важной характеристикой периодической ПШ последовательности её периодическая автокорреляционная функция, которая обычно определяется через слагаемые биполярной последовательности так

Ф(./) = 1;(2Л 1)(2Л.-1), 0<7< -1. (13.271)

где период. Ясно, что ф(7+ /7/) = ф(/) для любого целого г

В идеале псевдослучайная последовательность должна иметь автокорреляционную функцию со свойством ф(0) = и и ф(7) = О для 1 < / < « -1. В случае /«-последовательности периодическая функция автокорреляции равна

*(/) = {"• " (13 2.72)

1-1. (isy«" О

Для больших значений и, т.е. для длинных «/-последовательностей, величина отношения пиковых значений боковых лепестков ф(/) к пиковой величине функции

корреляции Ф(7)/Ф(0) -1/" мала и, с точки зрения практики, пренебрежима. Следовательно, ш-последовательность почти идеальная, если посмотреть с точки зрения корреляционной функции.

С точки зрения антипомеховых (АП) приложений ПШ широкополосных сигналов, период последовательности должен быть большим для того, чтобы затруднить источнику помехи изучить схему соединений в цепи обратной связи ПШ генератора. Однако, эго требование непрактично в большинстве случаев, поскольку поста1ювщик мешающего сигнала может определить соединения обратной связи путём наблюдения только 2т чипов ПШ последовательности. Эта уязвимость ПШ последовательности обусловлена линейными свойствами генератора Чтобы снизить уязвимость, выходные последовательности с отдельных ячеек регистра сдвига или выходы отдельных различных т последовательностей соединяются нелинейным путем, чтобы образовать нелинейную последовательность, которая значительно более трудна для изучения постановщиком помехи. Дальнейшее снижение уязвимости достигается путем частой смены соединений обратной связи и (или) числа ячеек регистра сдвига, в соответствие с заранее согласованным планом между передатчиком и заданным приемником.

В некоторых приложениях взаимокорреляционные свойства ПШ последовательностей столь же важны, как корреляционные свойства. Для примера, в CDMA каждому пользователю присваивается индивидуальная ПШ последовательность. В идеале ПШ последовательности отдельных пользователей должны быть взаимно ортогональны так, чтобы уровень интерференции, испытываемый одним пользователем от передачи других

пользователей, был бы равен нулю. Однако ПШ последовательности, используемые различными пользователями, на практике не обладают строгой ортогональностью.

Для конкретности, рассмотрим класс т-последовательностей. Известно (Сарвейт и Пурслей, 1980), что периодическая взаимокорреляционная функция между парой т последовательностей на том же периоде может иметь относительно большие пики. Таблица 13.2.1 дает пиковые амплитуды ф, для периодической функции взаимной

корреляции между парами /и-последовательностей для 3</w<12. Таблица также показывает число т последовательностей длины w = 2" -1 для 3 < /и < 12. Как мы можем видеть, число т последовательностей длины п быстро растет с т. Мы также видим, что для большинства последовательностей пиковые амплитуды взаимокорреляционной функции составляют большой процент от пикового значения автокорреляционной функции.

Таблица 13.2.1. Пиковые значения взаимной корреляции w-последовательностей и последовательностей Голда

Такие большие значения для взаимных корреляций нежелательны в CDMA. Хотя возможно выбрать малое подмножество т последовательностей, которые имеют относительно малые значения пиков взаимной корреляции, число последовательностей в этом подмножестве слишком мало для применений CDMA.

ПШ последовательности с лучшими свойствами периодической функции взаимной корреляции, чем т последовательности, даны Голдом (1967, 1968) и Касами (1966). Они образуются из т последовательностей, как описано ниже.

Голд и Касами доказали, что некоторые пары т последовательностей длины п имеют взаимно корреляционную функцию с тремя уровнями {-1, -tirn\ t{rn)-2\, где

Г2(-п/21 (нечёгные/и> /,...,.ч

()=1 . (13.2.73)

2(«.2)/21 (чётные w>

Для примера, если w = 10, тогда /(l0)=2*+l = 65 и три возможные значения

периодической взаимокорреляционной функции равны {-7,-65,63}. Таким образом, максимальное значения (по модулю) взаимной корреляции пары /-последовательностей равно 65, в то время как пик для семейства 60 возможных последовательностей,

40-56 625