13.13. Допустим, что (с,,} и -,>} является двумя двоичными (o,l) периодичсски.\н1 последовательностями с периодом Л/, и Л/ соответственно. Определите период последовательности, получаемой суммированием по niod 2 (с,,} и {с,,}.

13.14. Регистр сдвига максимальной длины с /и = 10 используется для генерирования псевдослучайно!! последовательности в широкополосной ПП системе. Длительность чипа 1\ 1мкс. а длительность бита (си.мвола) 7й - Л/7,., где ;V-длина (период) ;н-послсдовательности.

a) Определите выифыш обработки системы в децибелах.

b) Определите помехозащищенность, если требуемое Щ,! =10. а помеха является гармонической со средней мощностью .

13.15. Двоичная широкополосная ортогональнад система ЧМ при СЧ использует / = 15-ячеечный линейный сдвиговый регистр с обратными связями, который генсрир\ст последовательность макси.чмльной длины. К;1ждос состояние регистра сдвига выбир;1ст одщ из L неперекрывающихся частотных полосок. Битовая скорость - 100 бит/с. а скорость скачков - один на бит. Демодулятор использует нскогсрснтнос детектирование.

a) Определите полосу для скачков в этом канале.

b) Каков выигрыш обработки?

c) Какова вероятность ошибки в присутствии АБГШ?

13.16. Рассмотрите двоичную ортогональную систему с ФМ и СЧ, описанную в задаче 13.15. Предположим, что скорость скачков увели»шлась до 2 скачка/бит. Приемник использует квадратичное сложение для сложения сигналов от двух скачков.

a) Определите полосу скачков для канала.

b) Каков выифыш обработки?

c) Какова вероятность ошибки в присутствии АБГШ?

13.17. В широкополосной системе с быстрым СЧ информация передаётся посредством ЧМ с нскогерентным детектированием. Предположим, что и.меется Л = 3 скачка/бит и декодирование жёстких решений сигнала на каждом скачке.

a) Определите вероятность ошибки для этой системы в канале с АБГШ со спектральной плотностью мощности .V„ и 0СШ=13 дБ (общее ОСШ на три скачка).

b) Сравните результат а) с вероятностью ошибки широкополосной системы со СЧ, когда скачок совершается один раз на бит.

13.18. Широкополосная системе с медленным СЧ и двоичной ЧМ и некогерентным детектированием работает при IJ -10 с полосой скачков 2 ГГц и битовой скоростью 10 кбит/с.

a) Каков выифыш обработки системы?

b) Если помеха является парциально-полосовой, какая полоса занимается при наихудшей помехе"

c) Какова вероятность ошибки для случая наихудшей парциально-полосовой помехи?

13.19. Определите вероятность ошибки для широкополосной системы со СЧ, в которой используется двоичный свёрточный код в соединении с двоичной ЧМ. Интерференция в канале АБГШ. Выход дслюдулятора ЧМ подвергается квадратичному детектированию и проходит на декодер, который фор.\п1руст оптимальное декодирование мягких решений по Витерби, как описано в разделе 8.2. Предположите, что скорость скачков - 1 скачок на кодированный символ.

13.20. Повторите задачу 13.19 при декодировании жёстких решений по Витерби.

13.21. Повторите задачу 13.19, когда осуществляются быстрые скачки частоты со скоростью L скачков на кодированный символ.

13.22. Повторите задачу 13.19, когда осуществляются быстрые скачки частоты с L скачками на кодовый символ , а декодируются жёсткие решения по Витерби. L чипов на кодовом символе детектируется квадратично и сигналы складываются до принятия решения.

13.23. Сигнал TATS, описанный в разделе 13.3.3 демодулируется параллельным блоком из вось\ш согласованных ([)ильтров (восьмер№шая ЧМ) и выход каждого фильтра детектируется квадратично. Восемь выходов, полученных на каждом из семи сигнальных интерва.10в (общее число выходов 56) используется для формирования 64 воз.чожных величин решения, соответствующие коду Рида-Соломона (7,2). Определите верхнюю (объединённую) фаницу для вероятности ошибки кодового слова в канале с АБГШ при декодировании мягких решений.

13.24. Повторите задачу 13.23 для наи.худшего случая парциально-полосовой интерференции в канале. 13.2f?. Получите результаты (13.2.62) и (13.2.63) из (13.2.61).

13.26. Покажкте. чго (13.3.14) следует ю (13.3.13).

13.27. Получше (13.3.17) из (13.3.16).

13.28. Порождающие полиномы дпя конструирования кодовой последовательности Годда длины п=7 равны

8i(p)=P+P +

Генерируйте все последовательности Голда длины 7 и определиге взаимную коррелящоо одной последовательности с каждой другой.

13.29. В разделе 13.2.3 мы демонстрировали технику для расчёта вероягности ошибки кодовой системы с перемежением при импульсной интерференции, используя параметр предельной скорости Rq . Используйте кривые вероятности ошибки, данные на рис. Р13.29 при скорости сверточного кода 1/2 и ]/3 и декодировании мягких решений по Вигерби дпя опредедения соответствующих вероятностей ошибок дпя кодированной системы с импульсной интерференцией. Выполните расчёт дпя ЛГ = 3.5.7.

Объединенная граница Непрерывный гссовский шум Двоичная ФМ

Свёрточный код со скоростыо 1/3 Декодер Витерби Мягкие решения

а:=з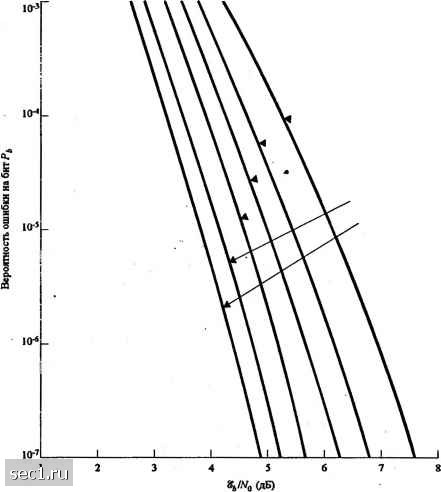

Рис. Р13.29

13.30. В кодированной и с перемежением ПП системе с двоичной ФМ при ПВМС и декодированием мягких решений предельно допустимая скорость равна Rq=1- logj G+oie"* ),

где a - доля времени, кйгда система под воздействием jamminga, % = %R, R - битовая скорость, я Nsj.

a) Покажите, чго ОСШ на бит Щ,Шо можно выразить так: = -1п-г--.

Nq oR 2"-1

b) Определите величину а, которая максимизирует требуемое %INq (случай наихудшего ПВМС) и резервирующее значение %INq.

с) Нарисуйте график lOlg/rA/o как функцию Лд, где г=Н/Я, ддя наих>дшего случая импульсной помехи и для АБГШ (а = l). Какие выводы вы сделаете относительно наихудшего воздействия ПВМС?

Объединённая граница Непрерывный гауесоаский шум Двоичная ФМ

Свёрточный код со скоростью 1 2 Декодер Витерби Мягкие решения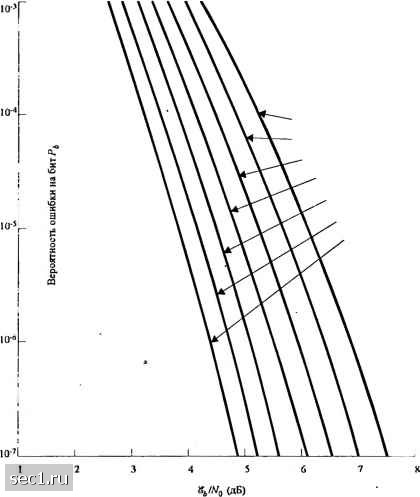

Рис. Р13.29 (продолжение)

13.31. В кодированной и с перемежением системе со скачками частоты и «у-ичной ЧМ с парциально-полосовой помехой и когерентной демодуляцией с декодированием мягких решений предельная скорость

/?o=log2

где а - доля полосы, поражённая помехой, Щ. - чиповая (одного тона) энергия, а -Jq.

а) Покажите, что ОСШ на бит можно выразить так:

(?-l)ot

b) Определите величину a, которая максимизирует требуемое %,INq (наи.\удший случай парциально-полосовой помехи) и результирующее значение Щ,1 Nq.

c) Определите rRIR в результате %/Nq из Ь) и нарисуйте график lOlg/ryVy как функцию от нормированной предельной скорости Rq /logj q ддя q = 2,4, 8,16, 32. Сравните эти графики с результато.м

задачи 13.30 с). Какие выводы вы делаете относительно воздействия наихудшей парциально-полосовой помехи? Какое влияние имеет увеличение объёма алфавита q ? Каковы потери в ОСШ между результатами задачи 13.30 с) и q -ичной ЧМ при q-co.