импульсные характеристики с(т;/) являются комплексным гауссовским случайным процессом по переменной /.

Многопутевая модель распространения для канала, воплощаемая в принимаемом сигнале /Д/) согласно (14.1.9), приводит к замиранию сигнала. Феномен замирания-

прежде всего результат изменений во времени фаз {9„(/)). Это означает, что случайные, меняющиеся во времени фазы {9„(/)}, связанные с векторами „е °", в определенный момент времени играют при суммировании векторов неблагоприятную роль. Когда это происходит, результирующий принимаемый сигнал /;(/) очень мал или практически равен

нулю. В другие моменты времени векторы з1„е "} складываются благоприятно, так чю

принимаемый сигнал большой. Таким образом, амплитудные изменения принимаемого сигнала, называемые замираниями сигнала, обусловлены переменными во времени многопутевыми характеристиками канала.

Когда импульсная характеристика с{х,1) моделируется как комплексный случайный

гауссовский процесс с нулевым средним, огибающая с(т;/) в любой момент /

распределена по Релею. В этом случае канал называют каналом с релеевскими замираниями В случае, когда имеются фиксированные рассеиватели или отражатели сигнала в среде в дополнение к случайно перемещающимся рассеивателям, с{г,1) нельзя моделировать процессом с нулевым средним. В этом случае огибающая б(т;/) имеет

райсовское распределение, и канал называют каналом с райсовскими замираниями. Другой функцией распределения, которая используется для моделирования огибающей сигнала, является «/-распределение Накагами. Эта модель замираний рассматривается в разделе 14.1.2.

14.1.1. Корреляционная функция канала и спектр мощности

Теперь рассмотрим некоторые используемые корреляционные функции и спектральные плотности мощности, которые определяют характеристики многопутевого

Если передастся узкополосный сигнал с полосой Л/ , и в модели (14.1.9) взаимное запаздывание ттсй та.хт.-т,«1/д/. \<ф1 ,-vq говорят о модели «однолучсвого» канала, а компоненты в (14.1.9) назыв:1ют «нодлуча.\1и». В «однолучсвой» модели разность фаз сигнала на различных частотах близка к нулю. Это приводит к неселективным по частоте замираниям сигнала. Если взаимное запаздывание п>тсй в принимасмо.м сигнале удовлетворяет условию тахт,-т, > 1/Д/, уф! , то говорят о многолучевой \юдсли

канала. Отдельные лучи в этом случае формируются сильно разнесенными нсоднородностями среды распространения, и посему сигналы отдельных лзчсй можно считать независимыми случайными процссса.хпг В «.многолучевой» raдeли разность фаз сигнала на различных частотах может существенно отличаться, что приводит к селективным по частоте замираниям сигнала. Весьма общей стохастической людслью «.многолучевого» радиоканала, имеющей наглядную физичсскто интерпретацию и подтвержденною экспери»1Снтально 6Г>. Г)7, является общая гауссовская .модель, согласно которой квадратурные компоненты в /-м луче -гД/) у/()ео5фД/). .Д/) = У/СОЧфД/) явл>иотся гауссовскими случайны\П1 процссса.хн1. Общая га\ссовскг1я .модель многолучевого канала разрабатывалась в 60-х годах Д.Д. Кловским и сго учсника.ми 66. 6S. 69. 70). С 1973 г. эта .\юдсль вошла в учебники по теории электросвязи 171/72]. Одно.мсрныс

распределения а.мплитуд yi=\xf+yf и фаз ф/= arctg(v;/x,) в этом случае называют

чстырёхпара метрическим и, поскольку» они зависят от четырёх параметров /н,.,, /н,.,, а,. ст;,. Модели

Раиса и Релея являются частными случая.ми 4-параметричсского распределения, а /н-распределение Накага\П1 для амплитуд сигнала можно считать аппрокси.мацией 4-парамстрического распределения 66] (прп).

канала с замираниями. Нашей исходной точкой является эквивалентная низкочастотная импульсная характеристика c(t;/), которая характеризуется как комплексный случайный процесс по переменной /. Предположим, что процесс c(x,i) стационарен в широком смысле. Тогда мы определяем автокорреляционную функцию с(т,() так:

ФХх„с,;А/) = 14Чт,;0Ф2; + А/)].

(14.1.10)

в большинстве сред, где передается радиосигнал, ослабление и сдвиг фазы в канале, связанные с задержкой в пути t,, некоррелированы с ослаблением и сдвигом фазы, связанными с задержкой в пути т,. Это обычно называется некоррелированным рассеянием. Мы сделаем предположение, что рассеяния при двух различных задержках некоррелированы, и учтем это в (14.1.10), чтобы получить

4сЧх,;0Ф2;+А0]=Фс(.;Д)5(х,-т2). (14.1.11)

Если возьмем Д/ = 0, результирующая автокорреляционная функция Фс(с;0) = ф(т)-это просто средняя мощность выхода канала как функция от задержки во времени т. Из этих соображений ф<,(х) называют интенсивностью многопутевого профиля или спектром

моицности задержек канала. В общем ф(т;А/) определяет среднюю мощность выхода канала как функцию от времени задержки х и разницы моментов наблюдения Д/. На практике функция ф(т;А/) измеряется путем передачи по каналу очень короткого импульса и вычислением взаимной корреляции принимаемого сигнала со своей собственной запаздывающей копией. Можно ожидать, что измеренная функция ф.(х)

имеет типичный вид, показанный на рис. 14.1.2. Область значений, в которой ф(т) существенно больше нуля, нгзъи&ают многопутевым рассеянием канала и обозначают Г„,.

Полную характеристику многопутевого переменного во времени канала можно определить и в частотной области. Взяв преобразование Фурье от с(х;/), мы получаем переменную во времени передаточную функцию C{J;i), где /-частотная переменная. Итак,

С(/;0 = £ф;/)е->Л. (14.1.12)

В предположении, что канал стационарен в широком смысле, мы определим автокорреляционную функцию

ФсС/,./2;Д0 = 1£[С(У;;0С(Л;/+А0]-

Рис. 14.1.2. Профиль многопутевой интенсишости (14.1.13)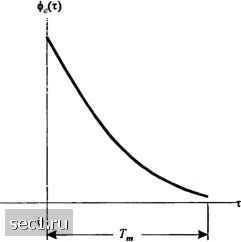

Поскольку С(/;/) является преобразованием Фурье от с(х;/), то не является неожиданностью, что Фс(/./2;А0 связано с ф(т;Д/) преобразованием Фурье. Это соотношение легко получить подстановкой (14.1.12) в (14.1.13)

(14.1.14)

= Г"фДт,;Д05(т,-т,)е"-ЧЛ2

- оо J-со

-00 J- 00

= г г фДт.; Д/)е-У-Jx, = ф,(Д/; ДО, где Д/ = /,-/. Из (14.1.14) мы видим, что ф.(/У;Д/) является преобразованием Фурье от

многопутевой интенсивности профиля. Далее, из предположения, что рассеяние некоррелировано (по отдельным путям) следует, что автокорреляционная функция от C{f,t) по частоте зависит только от разности частот Af = f.-f. Следовательно, подобает называть ф.(Д/; Д/) совместной корреляционной (pyuKifueu канала в частотной и

временной области. На практике ее можно измерить путем передачи по каналу двух синусоид с частотным разносом Д/" и измерением взаимной корреляции двух отдельно принимаемых сигналов с временной задержкой между ними Д/.

Предположим, что возьмём в (14.1.14) Дг = 0. Тогда ф (Д/"; 0) = ф. (Д/), и фдх;0) S ф(т), связь между ними упрощается:

Фс(Д/)=ГфДт)е dx. Это соотношение отображено графически на рис. 14.1.3.

(14.1.15)

Н«с(4/)1

Пара

Карреляцио1шая функция в частотной области

преобразований Фурье

Профиль многопутевой иитснсивности Рис. 14.1.3. Соотношение между Фс(4/)1 ч ФД)

Поскольку ф(,(Д/) является автокорреляционной функцией по частотной переменной, она обеспечивает нам возможность измерить частотную когерентность канала. Как следствие преобразования Фурье между ф(,(Д/) и ф(х), обратная величина многопутевого

рассеяния является мерой частотной когерентности канала. Это значит, что

т.-, (14.1.16)