где (А/")с означает полосу частотной когерентности. Таким образом, две синусоиды с частотным разносом, большим (А/"), ведут себя различно в канале. Если (А/") мало по сравнению с полосой частот переданного сигнала, канал называют частотно селективным В этом случае сигнал существенно искажается в канале. С другой стороны, если (А/")

велика по сравнению с полосой частот переданного сигнала, канал называют частотно неселективным.

Теперь сосредоточим наше внимание на изменении канала во времени, измеряемом параметром А/ в фс(Д;Д/). Изменения во времени характеристик канала

свидетельствуют о доплеровском рассеянии и, возможно, также о сдвиге спектральных линий. Чтобы выявить связь эффекта Доплера и изменений во времени канала, определим преобразование Фурье от фс(4/";Д/) по переменной А/, чтобы получить функцию S,W-X).T.c.

5е(Л/;Х) = f" фе(Д/; Д/)е-"с/Д/. (14.1.17)

При ДГ = О 5е(0;) = ScQC), и из (14.1.17) следуег

5е() = £фс(А)е""А/. (14.1.18)

Функция ScQC) определяет спектр мощности и дает интенсивность сигнала как функцию от частоты Доплера X. Поэтому SQC) называют доплеровским спектром мощности канала.

Из (14.1.18) мы видим, что если канал не меняется во времени, фс(А/) = А, и функция 5с (Я,) становится равной КЪ{Х). Следовательно, когда нет изменений канала во времени, не наблюдается спектральное расширение при передаче чистого тона.

Область значений X, в которой SQC) существенно отлично от нуля, называют

доплеровским рассеянием в канале Bj. Поскольку SQ) связано с Фс(Д/)

преобразованием Фурье, обратная величина является мерой временной когерентности канала, т.е.

(А/),«-, (14.1.19)

где (Л/) называют временем когерентности. Ясно, что канал с медленными изменениями имеет большую временную когерентность или, что эквивалентно, малое доплеровское рассеяние. Рис. 14.1.4 иллюстрирует соотношение между Фс(Д/) и SQ).

Теперь мы установим соотношение Фурье между фс(А/";Д/) и ф(т;Д/), включающих переменные (т.Д/), и между фс(Д/";Д/) и 5(4/";А,), включающих переменные (Jl,X). Имеются два дополнительных преобразований Фурье, которые мы можем найти и которые служат для связи ф(т;Д/) и iSc(/V;A,), и таким образом замыкается цепь. Требуемое отношение можно получить, определив новую функцию, обозначаемую 5(т;А,), как преобразование Фурье ф(х;Д/) попеременной Д/,т.е.

S(r,X)= ГфДх;Дт)е--""б/Д/. (14.1.20)

Отсюда следует, что 5(х;Х) и Sc(M,) являются парой преобразований Фурье. То есть

S{%X) = Г 5e(A/;X)e-c/Y - .(14.1.21)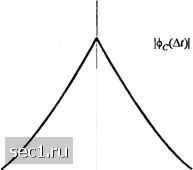

Пара

преобразований Фурье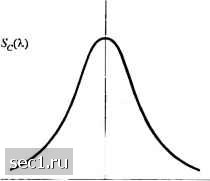

Корреляционная функция во временной области Спектр доплеровскога рассеяния

Рис. 14.1.4. Соотношение между фс(Д01 и

Далее, 5(х; А.) и ф, (А/; At) связаны двойным преобразованием Фурье

S(r,X) = Г Гфс(Д/";А/)е ""е"АйА/. (14.1.22)

Эту новую функцию S(t,X) называют функцией рассеяния канала. Она определяет меру средней мощности на выходе канала, как функцию времени задержки т и доплеровской частоты X.

Соотношения между четырьмя функциями фр(/У;А/), ф(т;А/), <(,(А/;Х) и S(t,X)

подытожены рисунком 14.1.5.

Функция рассеяния S(t,X), измеренная на тропосферной линии рассеяния протяженностью 150 миль, показана на рис.14.1.6. Сигнал, использованный для зондирования канала, имеет разрешение во времени 0,1 мкс. Поэтому ось для времени запаздывания проквантована с шагом 0,1 мкс. Из рисунка мы видим, что многопутевое рассеяние равно Г, = 0,7 мкс. С другой стороны, доплеровское рассеяние, которое можно

определить как полосу спектра мощности для каждого пути сигнала на уровне 3 дб, оказывается переменной для каждого сигнального пути. Для примера, в одном пути оно меньше 1 Гц в то время как в некоторых других путях оно составляет несколько герц. Для наших целей мы.возьмем наибольшее рассеяние по различным путям на уровне 3 дб и назовем ее доплеровским рассеянием.

14.1.2. Статистические модели для каналов с замираниями

Имеются несколько распределений вероятности, которые следует рассмотреть при конструировании модели статистических характеристик канала с замираниями. Когда имеется большое число рассеивателей в канале, которые образуют сигнал на приеме, как в случае ионосферного или тропосферного распространения сигнала, применение центральной предельной теоремы вероятностей приводит к гауссовской модели для характеристики канала. Если процесс с нулевым средним, тогда огибающая характеристики канала в любой момент времени имеют релеевское распределение вероятностей, а фаза распределена равномерно на интервале (0,2л). Релеевское распределение можно записать в виде

Ря(/-) = е-/", г>0, (14.1.23)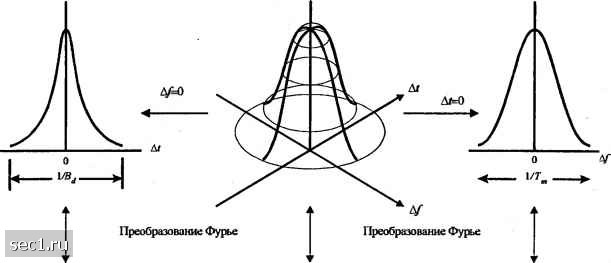

S(/,X)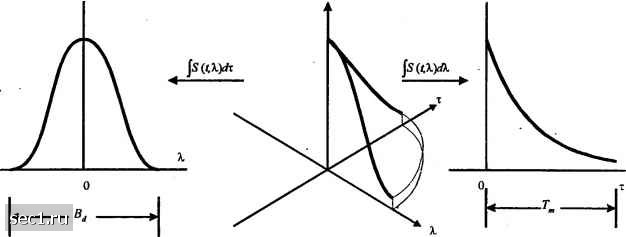

Рис. 14.1.5. Со(т10шение межзу корреляхщониой функцией канала и функцией рассеяния [Gtven (1%2)]

a = E(R). (14.1.24)

Мы видим, что релеевское распределение характеризуется единственным параметром

Альтернативной статистической моделью для огибающей характеристики канала является -распределение Накагами, определяемое ФПВ (2.1.14). В противовес распределению Релея с единственным параметром, который можно использовать для оценки статистики канала с замираниями, -распределение Накагами является двухпараметрическим, именно, включает параметр т и второй момент Q = E(R). Как

следствие, w-распределение позволяет более гибко и точно оценить наблюдаемую статистику сигнала. Его можно использовать для моделирования условий замираний в канале, которые являются более или менее глубокими, чем определяемые законом Релея, и оно включает распределение Релея как частный случай (/и=1). Для примера, Турин (1972) и