/(jc;) = -log,2-*=A: бит, и она выдаётся на временном интервале Кх. Таким образом, логарифмическая мера количества информации обладает желаемыми свойствами аддитивности, когда определённое число единичных выходов источника рассматривается как один блок.

Теперь вернёмся к определению взаимной информации, определяемой (3.2.1), и

умножим числитель и знаменатель отношения вероятностей на •

Р{хАу,) Р{х,\у)Р{у,) P(x„yj) P(yJx,) Р{х,) Р{х,)Р{у) P(,x,)Piyj) Р(у)

Отсюда делаем вывод

1(х,;у) = 1(у/,х,). (3.2.4)

Таким образом, информация, содержащаяся в выборе события Y=yj относительно события Хх„ идентична информации, содержащейся в выборе события Х=х, относительно события Y=yj.

Пример 3.2.2. Предположим, что X и К-двоичные {0,1} случайные величины, представляющие вход и выход канала с двоичным входом и двоичным выходом. Входные символы равновероятны, а условные вероятности выходных символов при заданном входе определяются так:

P(Y = 0\X = Q)=\-p„

PiY = l\XQ) = Po.

Р(У = 1 = 1) = 1-А. P(Y = 0\X = \) = p,.

Определим, сколько информации об X = О и = 1 содержится в событии У = 0. Из заданных вероятностей получим

PY 0) = Р{У 0\Х = 0)Р(Х = 0) + PiY = 0\Х = 1)Р{Х = 1) \(\-р+ р,);

PiYl) = P(Yl\X = 0)PiX = 0) + PiY = \\X = l)PiX = \)il-p,+p,).

Тогда взаимная информация о символе = О при условии, что наблюдается У= О, равна

(jc,;y,) = /(0;0) = log, =1оё2

Р(У = 0)

Аналогично взаимная информация о символе А=1 при условии, что наблюдается У= О, равна

/(;c,;y,) = /(l;0) = log .

Рассмотрим несколько частных случаев. В первом, когда Pq= р, = 0, канал называют каналом без шумов и 7(0; 0) = log, 2 = 1 бит.

Следовательно, когда выход точно определяет вход, нет потери информации. С другой стороны, если Ро = р, -1/2, канал становится непригодным так как 7(0;0) - log, 1 = О.

Если Ро = р, = 1 / 4, то

7(0;0) = log, =0,587 бит; 7(0;l) = log,i = -16HT.

Этот случай называют «обрыв канала» (прп)

Помимо определения взаимной информации и собственной информации полезно определить условную собственную информацию как

1{х, \у) = log--= -logP(>:, \yj). (3.2.5)

Тогда, комбинируя (3.2.1), (3.2.3) и (3.2.5), получаем соотношение

I{x-yj) = I{x,)-I{x,\y). (3.2.6)

Мы интерпретируем /(х ) как собственную информацию о событии Х=х, после наблюдения события У=уу. Из условия /(х,)>0 и /(х, >,)>0 следует, что /(х,.>)<0, когда /(х,. !>-,)>/(х,.), и /(х,,>,)>0, когда/(х,. >»,)</(х,). Следовательно, взаимная информация между парой событий может быть или положительной, или отрицательной, или равной нулю.

3.2.1. Средняя взаимная информация и энтропия

Зная взаимную информацию, связанную с парой событий (л;,,,), которые являются возмолсной реализацией двух случайных величин X и Y, мы можем получить среднее значение взаимной информации простым взвешиванием 1{х,у) с вероятностыо"

появления этой пары и суммированием по всем возможным событиям. Таким образом, получим

" " " * Р(х V )

nX-Y) = YYnx.,y,mx,,y) = Y.i:n.yj)<eji (3-2.7)

как среднюю взаимную информацию между X и Y.

Видно, что l{X,у) = О, когдаXuYстатистически независимы и Р(х,,yj) = Р(х,)Р(у,).

Важным свойством средней взаимной информации является то, что I{X,Y)>0 (см. задачу 3.4).

Аналогично определим среднюю собственную информацию, обозначенную Н(Х):

Н(Х) = XР{х,)/(х ) = -X()log() (3-2-8)

1-1 .-I

Если А" представляет собой алфавит возможных символов источника, Н(Х) представляет среднюю собственную информацию на символ источника, и её называют энтропией источника. В частном случае, когда символы источника равновероятны, Р{х,)=\/п для

всех г, и, следовательно,

HiX) = -filogj; = logn. (3.2.9)

В общем случае H{x)<\ogn (см. задачу 3.5) при любых заданных вероятностях символов источника. Другими словами, энтропия источника максимальна, когда выходные символы равновероятны.

Пример 3.2.3. Рассмотрим двоичный источник, который выдаёт последовательность независимых символов, причём выходной кодовый символ «О» с вероятностью q, а символ «1» с вероятностью \-q. Энтропия такого источника

Термин «энтропия» взят из механики (термодинамики), где функция, похожая на (3.2.8), названа (термодинамической) энтропией.

Н{Х) -Hicj) = -q log q-(\-g) log(l - q) .

(3.2.10)

Функцию H(g) иллюстрирует рис. 3.2.1. Видно, что максимальное значение функции энтропии имеет место при q = j, причём Я(у)= 1 бит.

Среднее значение условной собственной информации называется условной энтропией и определяется как

(in = IZm,>.,)Iog-1-. (3.2.11)

Мы интерпретируем н[х у) как неопределённость X (дополнительную информацию,

содержащуюся в X) после наблюдения Y

Комбинация (3.2.7), (3.2.8) и (3.2.11) даёт соотношение

I{X;Y) = H(X)-H(X\Y)H(Y)-H{Y\X). (3.2.12)

Из условия следует, что

H{x)>h(x\y) и h{y)>h{y\x), причём

равенство имеет место тогда, и только тогда, когда X и Y статистически незави-симы. Если мы интерпретируем н[х\у) как

среднее значение неопределённости (условной собственной информации) X после наблюдения Y и Н{х) как среднее значение априорной неопределённости (собственной информации), т.е. имевшейся до наблюдения, тогда I{X,Y) определяет взаимную информацию (уменьшение среднего значения неопределённости, имеющейся относительно X после наблюдения У). Так как h{x)>h{x\y), то ясно, что при условии

наблюдения У энтропия Н{х) не увеличится.

Пример 3.2.4. Определим я(ху) и I{X,Y) для канала с двоичным входом и выходом, рассмотренного выше в примере 3.2.2, для случая, когда Ро= Pi= Р- Пусть вероятность входных символов равна p{X = Q) = q и P{X\)l-q .Тогда

Н{Х) H{q) =-q\gq-{\- q)\g{\ - q),

где Я(9) - функция энтропии, а условная энтропия я(у) определяется (3.2.11). Зависимость h{x\y) в бит/символ как функция от и параметра р показана на рис. 3.2.2. График средней взаимной информации I{X,Y) в бит/символ дан на рис. 3.2.3.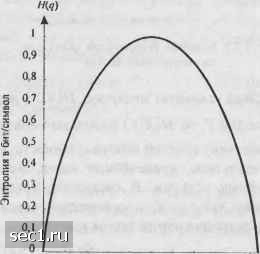

о 0.1 0,2 0.3 0,4 0,5 0,6 0.7 0,8 0.9 1 Вероятность q

Рис. 3.2.1. Энтропия двоичного источника