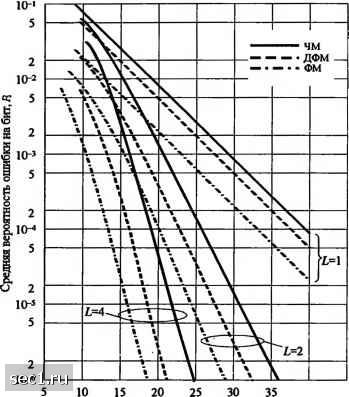15 20 25 30 Среднее ОСШ % (дБ)

Рис. 14.4.2. Качество двоичных сигналов с разнесением 14.4.2. Многофазные сигйалы

В приложении С детально рассматривается передача многофазных сигналов через канал с релеевскими замираниями. Наша основная цель в этом разделе привести общие результаты для вероягности ошибки на символ в Л/-ичной ФМ и ДФМ и для вероятности ошибки на бит в четырёхфазной ФМ и ДФМ. Общий результат для вероятности ошибки на символ для А/-ИЧНОЙ ФМ и ДФМ

\xsm(n/M)

(э- f 1

(M-iy

1--=-- arcctg=- -

V* - cos (п/М) -jb - р cos (п/М) J

-pC0s(7t/M)

(14.4.35)

1 + Ус

для когерентной ФМ (для ФМ при когерентном приеме) и

1 + Ус

(14.4.36)

(14.4.37)

для ДФМ. Опять это среднее значение ОСШ на канал. ОСШ на бит у,, =Ly/k, где k = logM.

Вероягность ошибки на бит для четырёхфазной ФМ и ДФМ получена в предположении, что пара информационньпс бита отображается в четыре фазы согласно коду Грея. Выражение для вероятности ошибки на бит, полученное в приложении С, равно

(14.4.38)

где л,-снова определяется (14.4.36) и (14.4.37) для ФМ и ДФМ соответственно.

Рис. 14.4.3 иллюстрирует вероятность ошибки на символ для ДФМ и когерентной ФМ при = 2, 4, 8 и L = 1. Заметим, что разница в качестве между ДФМ и когерентной ФМ равна примерно 3 дБ для всех значений М Действительно, когда Уь » 1 и L = 1, (14.4.35) хорошо аппроксимируется так

(14.4.39)

(Mlog2M)[sin-(7r/M)Jy,

(14.4.40)

для ДФМ и

р М-1

*~(Mlog,M)[sin47c/M)j2Y,

для ФМ. Таким образом, при больших ОСШ когерентная ФМ на 3 дБ лучше, чем ДФМ, в канале с релеевскими замираниями. Эта разница также сохраняется при увеличении L.

Вероятность ошибки на бит отображается на рис. 14.4.4 для двухфазовой, четырёхфазной и восьмифазной ДФМ при /.-1,2,4.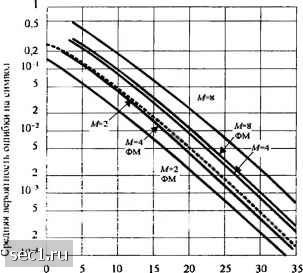

10 5

"10- 5

10 5

10-" 5

10- 5

10-«

10 15 20 25 Среднее ОСШ у» (дБ) Рис. 14.4.3. Средняя вероятность ошибки на символ для ФМ и ДФМ в релеевском канале

10 15 20 25 30 Среднее ОСШ Yj (дБ)

Рис. 14.4.4. Вероятность ошибки на бит для ДФМ в релеевском канале с разнесением

Выражение для вероятности ошибки на бит восьмифазной ДФМ с кодом Грея здесь не дается, но она имеется в статье Прокиса (1968). В этом случае мы видим, что качество для двух- и четырёхфазной ДФМ приблизительно одинаково, в то время как восьмифазная ДФМ на 3 дБ хуже . Хотя мы не привели вероятность ошибки на бит для когерентной ФМ, можно показать, что 2- и 4-фазные когерентные ФМ имеет примерно одинаковое качество.

14.4.3. М-позиционные ортогональные сигналы

В этом подразделе мы определим качество Л/-ичной ортогональной системы сигналов, передаваемых по каналу с релеевскими замираниями, и оценим выгоду сигналов с

большим объёмом алфавита М относительно двоичных. Ортогональные сигналы можно рассматривать как сигналы М-ичной ЧМ с минимальным разносом частот 1/7", где Т-сигнальный интервал. Сигнал с той же информацией передается по L разнесенным каналам. Каждый разнесенный канал считается частотно-неселективным и с медленными замираниями, а процесс замираний по L каналам считается статистически взаимно независимым. В каждом канале сигнал искажается аддитивным белым гауссовским шумом. Считаем, что эти аддитивные шумовые процессы статистически независимы.

Хотя относительно легко сформулировать структуру и выполнить анализ качества сумматора с максимальным отношением для разнесенных каналов с М-ичными сигналами, более вероятно, что разработчик выберет некогерентное детектирование. Следовательно, мы обратим наше внимание на квадратичное сложение разнесенных сигналов. Выход сумматора, содержащего сигнал, равен

f/, =5]2&Xte--*+i\t, , (14.4.41)

в то время как выходы остальных сумматоров

f/» =Z КГ. " = 2,3, 4,...,М. (14.4.42)

Вероятность ошибки равно 1 минус вероятность того, что С/, > U„ для /м = 2, 3, . Поскольку сигналы ортогональны, а аддитивный шумовой процесс в отдельных каналах разнесения статистически независим, случайные величины U,u2,...,Uf также статистически независимы. ФПВ для (/, определяется (14.4.31). С другой стороны u2,...,U одинаково распределены с функцией плотности вероятности, определяемой (14.4.32). При фиксированном f/, совместная вероятность P{lJ2<U,U<U,...,U„<U) равна вероятности Р((/2 <f/,) в степени М-\. Теперь

i-l 1

(14.4.43)

где a\ = 2Ша. Чтобы получить вероятность правильного приема, (М -1)-я степень от этой

вероятности затем усредняется по f/,.

Если мы вычтем этот результат из 1, мы получим вероятность ошибки в виде, данном Ханом (1962):

(2af)4l-l)

f/," ехр

ч 2ah

1-ехр

2о\) 1

l-e-Z

(l + Y.f(Z.-l>

-f/expf-

(14.4.44)

где - среднее ОСШ на канал разнесения. Среднее ОСШ на бит Уь = Ly/Xogj М - Ly/k .

Интеграл в (14.4.44) можно выразить в замкнутой форме через двойную сумму. Это можно показать, если написать