n,(L-\) к=0

(14.4.45)

где Р„,- набор коэффициентов. Тогда (14.4.44) приводится к виду

Рм =

n,(L-\) *=0

1 + Yc

(14.4.46)

---У-

Если нет разнесения (/- = l), вероятность ошибки (14.4.46) приводит к простой форме

,(-1Г

(14 4.47)

\ + т +

Вероятность ошибки символа 7, можно преобразовать в эквивалентную вероятность ошибки на бит, умножая на 2*"/(2* -l).

Хотя выражение для (14.4.46) находится в замкнутой форме, оно затруднительно для вычислений для больших значений МиЬ.

Альтернативно можно вычислить численным интегрированием, используя выражение (14.4.44). Результаты, иллюстрируемые ниже на графиках, были получены из (14.4.44).

Сначала рассмотрим вероятность ошибки для М-ичной ортогональной системы сигналов с квадратичным сложением, как функция от порядка разнесения. Рис. 14.4.5 и 14.4.6 иллюстрируют характеристики Рм для М=2 и 4, как функция L, когда суммарное ОСШ, определенное как у = Z-Y, остается фиксированным. Эти

результаты указывают на то, что имеется оптимальный порядок разнесения для каждого Yl Это значит, что для любого имеется величина L, при которой 7 минимальна. Тщательное исследование этих графиков обнаруживает, что минимум 7 получается, когда Y=Y,/7-«3. Оказывается, что этот результат не зависит от объёма алфавита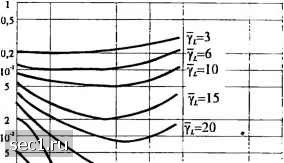

10" 5

10" 5

5 2 5 2

2 3 5 10 20 Порядок разнесения, l

Рис. 14.4.5. Характеристика двоичных ортогонильных сигналои при квадратичном детектировании с разнесением

Во-вторых, рассмотрим вероятность ошибки как функцию от среднего ОСШ на бит, определяемого y=LyJk. (Если мы интерпретируем

Л/-ичную ортогональную ЧМ как форму кодирования, а порядок разнесения L как число повторений символа в коде с повторением, тогда Yi = Ус /К. где R=k/L- скорость кода). Зависимость от у, для

Л/ = 2, 4, 8, 16, 32 и L = l, 2, 4 показаны на рис. 14.4.7.

Эти результаты иллюстрируют выигрыш в качестве по мере роста М и L. Сначала заметим, что достаточный выигрыш в качестве получается при увеличении L. Второе, мы заметим, что выигрыш в качестве при росте М относительно небольшой при малых L. Однако при увеличении L выигрыш, получаемый с ростом М, также растёт. Поскольку увеличение любого из этих параметров влияет на полосу частот, так как

В logjM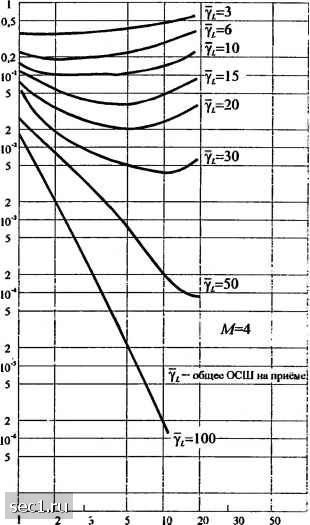

3 5 10 20 Порядок разнесения. L

Рис. 14.4.6. Характеристика ортогональных сигна-юв с А/ = 4 при квадратичном детектировании с разнесением

ТО результаты, показанные на рис. 14.4.7, указывает на то, что увеличение L более эффективно, чем соответствующее увеличением

Как мы увидим в разделе 14.6, кодирование является эффективным по полосе частот средством для получения разнесения сигнала, переданного по каналу с замираниями.

Граница Чернова. Перед окончанием этого раздела, мы определим верхнюю границу Чернова для вероятности ошибки двоичной ортогональной системы сигналов с разнесением Z,-ro порядка, которое будет полезным в нашем обсуждении кодирования для каналов с замираниями, что является предметом раздела 14.6. Наша исходная точка это выражение для двух величин для решения (/, и U, определяемых (14.4.29), где U,

содержит слагаемые сигнала и шума при квадратном суммировании, а содержит только слагаемые шума при квадратичном суммировании. Вероятность ошибки двоичной системы сигналов, обозначенная здесь /2()> равна

P,(L)=P(U,-U, >0)=P{X>Q) = [p{x)dx, где случайная величина X определена так

(14.4.48)

В разделе 14.6 мы покажем, чго А/-ичную ортогональную систему ЧМ с разнесением можно рассматривать как блоковый ортогональный коя

Фазовые слагаемые

(14.4.49)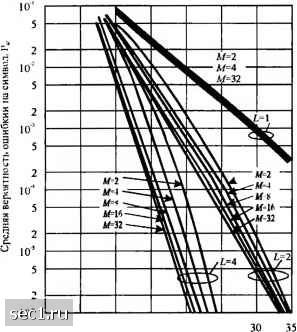

10 15 20 25 Среднее ОСШу» (дБ)

Рис 14 4.7. Помехоустойчивость передачи с использованием Л/-ПОЗИЦИОН11ЫХ ортогональных сигаалов при А-кратном разнесении

(Фк) в (/, опущены, так как они не влияют на качество при квадратичном

детектировании.

Пусть S{X) означает единичную функцию. Тогда вероятность ошибки в (14.4.48) можно выразить в виде

P{l) = E[S{X)]. (14.4.50)

Согласно разделу 2.1.5, граница Чернова ограничивает сверху единичную функцию экспоненциальной функцией, т.е.

S{X)<Q, Q>0, (14.4.51)

где параметр С, оптимизируется для получения плотной границы. Таким образом, мы имеем

P{l)=E[SiX)\<E(e). (14.4.52) Если вместо случайной величины X подставим (14.4.49) и учтём, что случайные слагаемые в сумме статистически независимы, получаем результат

1-2СаГ

1 + 2Са;

(14.4.53)

(14.4.54)

(14.4.55)

где а; = 2(?#„, а; = 2рЛо(1 + у), а - среднее ОСШ на канал разнесения. Заметим, что а; и а] не зависят от к, т.е. параметры аддитивного шума в L разнесённых каналах, как и его распределение, одинаковы. Следовательно (14.4.53) приводит к

Дифференцируя правую часть (14.4.56) по С,, находим, что верхняя граница минимизируется, если

(14.4.57)

- .2 2

Подстановка (14.4.57) для С, в (14.4.56) даёт верхнюю границу Чернова в виде