(14.4.58)

4(1 +yJ L(2+yJJ

Интересно отметить, что (14.4.58) можно также выразить так

P,(L)<[4p(l-p)f (14.4.59)

где p = l/(+yJ) - вероятность ошибки для двоичных ортогональных сигналов в канале с

замираниями без разнесения.

Сравнение границы Чернова (14.4.58) с точным, значением вероятности ошибки для двоичной ортогональной системы сигналов, при квадратичном сложении по L каналам разнесения, определяемым формулой

С 1 Vi-/Л-l + Yl+v Y -CL-l+kЛ

(14.4.60)

обнаруживает достаточную плотность найденной границы. Рис. 14.4.8 иллюстрирует сравнение. Мы видим, что верхняя граница Чернова отличается примерно на 6 дБ от точных значений вероятности ошибки при /, = 1, но по мере роста L она становится плотнее. Дпя примера, разница между границей и точным значением вероятности ошибки равна примерно 2,5 дБ при Z, = 4.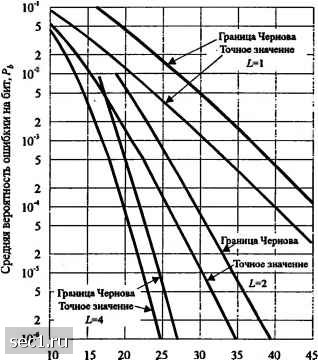

Среднее ОСШ

Рис. 14.4.8. Сравнение границы Чернова с точным значением вероягности ошибки

В заключение мы напомним, что вероятность ошибки для М-ичной ортогональной системы сигналов с разнесением можно оценить сверху объединённой границей

Р<(М-\Ш11 (14.4.61)

где P,(Z,) определяется или точным значением (14.4.60), или границей Чернова (14.4.58).

14.5. цифровая передача по частотно-селективному каналу с медленными замираниями

Когда фактор рассеяния канала удовлетворяет условию T„,Bj «1, возможно выбрать сигналы, имеющие полосу W « (А/\ и длительность 7« {At\. Это значит, что канал

частотно-неселективен и с медленными замираниями. В таком канале можно использовать технику разнесения, чтобы преодолеть тяжёлые последствия замираний.

Если полоса W »{А/\, удобно для пользователя разделить канал на определённое число частотно-разделённых (FDM) подканалов, имеющих взаимное расстояние центральных частот по крайней мере {А/\. Затем один и тот же сигнал можно передать по

всем FDM подканалам и, таким образом, получается частотное разнесение. В этом разделе мы опишем альтернативный метод.

14.5.1. Модель канала в виде линии задержки с отводами

Как мы теперь покажем, более прямой метод для достижения по существу того же результата сводится к использованию широкополосного сигнала, заполняющего полосу частот Ж. Канал по-прежнему считается с медленным замираниями при выполнении условия T«{Ai\.. Теперь предположим, что W-это полоса частот, занимаемая реальным полосовым сигналом. Тогда полоса частот, занимаемая эквивалентным низкочастотным сигналом s,{t), равна / <W. Поскольку s,{t) ограничен по полосе

\f<\W, использование теоремы отсчётов приводит к представлению сигнала

sm[nW(t-»/W)]

nW{t-nlW)

(14.5.4)

Преобразование Фурье для s,{i) равно

f <-w

/ >-w

(14.5.2)

Принимаемый сигнал без шума в частотно-селективном канале был раньше представлен в виде

Г C(/-t)S,if)e"df, (14.5.3)

где C{f\i) - переменная во времени передаточная функция канала. Подстановка (14.5.2) для s,{f) в (14.5.3) даёт

-ДО = Т Z sXulW)\y{jjy df = ±sXnlW)c{t-nlW,l), (14.5.4)

где с(х;/) - переменная во времени импульсная характеристика канала. (14.5.4) имеет форму свёртки. Её можно выразить в альтернативной форме

rif)=-Y,s,{t-nlw)c{nlW-t).

(14.5.5)

Удобно определить ансамбль переменных во времени коэффициентов канала так

Тогда (14.5.5), выраженная через эти коэффициенты канала, принимают вид

r(0=f,c„(t)sfy-n/W). (14.5.7)

/1=-со

Форма принимаемого сигнала (14.5.7) подразумевает, что переменный во времени частотно-селективный сигнал можно моделировать или представить как линию задержки с отводами, задержка между которыми равна \/W, и со взвешивающими коэффициентами {с„(/)}. Действительно, мы заключаем из (14.5.7), что низкочастотная импульсная характеристика канала равна

c{t;t)= ;c„(/)5(t-,i/Pr), (14.5.8)

(14.5.9)

а соответствующая переменная во времени передаточная функция

Итак, при помощи эквивалентного низкочастотного сигнала с полосой , где 1¥»{А/\у мы достигаем разрешение во времени ]/W по многопутевому профилю запаздывания. Поскольку суммарное многопутевое рассеяние равно Т, для всех практических целей модель канала на линии задержки можно сконструировать на L = [7„Ж]+1 ячеек. Тогда принимаемый сигнал без шума можно выразить в виде

(14.5.10)

Сконструированная модель линии задержки с отводами показана на рис. 14.5.1.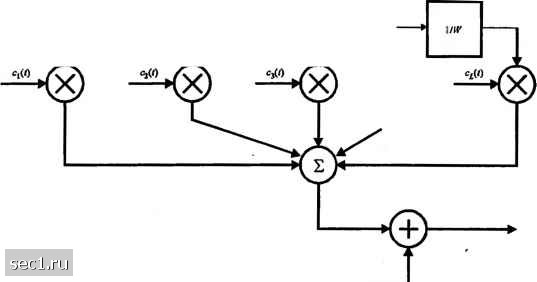

Рис. 14.5.1. Модель частотноч:елекгивного канала на основе линии задержки с отводами

Аддитившя помеш