в соответствии со статистической характеристикой, представленной в разделе 14.1, переменные во времени веса в отводах являются стационарными комплексными

случайными процессами. В частном случае релеевских замираний амплитуды с„(/) = а„(/) распределены по Релею, а фазы ф„(0 имеют равномерное распределение. Поскольку {c„{t)} представляет веса отводов, соответствующих L различным задержкам х = «/Ж, = 1,2,...,L, предположение о некоррелированном рассеянии, сделанное в разделе 7.1, предполагает, что процессы {c„{t)} взаимно некоррелированы. Когда {с„(/)} гауссовские случайные процессы, они также статистически независимы.

14.5.2. RAKE демодулятор

Теперь рассмотрим проблему цифровой передачи по частотно-селективному каналу, который моделируется линией задержки с отводами и со статистически независимыми, меняющимися во времени, весами Очевидно, однако, в самом начале, что модель

линии задержки с отводами со статистически независимыми весами отводов даёт нам L образцов одного и того же переданного сигнала. Следовательно, приёмник, который обрабатывает принимаемый сигнал оптимальным образом, может достичь качества эквивалентной системы связи с разнесением L-ro порядка.

Рассмотрим двоичную передачу по каналу. Мы имеем два сигнала равной энергии .v„(/) и .v,-,(/), которые или противоположные или ортогональные. Их длительность Т

выбирается так, чтобы удовлетворять условию Т»7. Таким образом, мы можем

пренебречь межсимвольной интерференцией, обусловленной многопутёвостью. Поскольку полоса сигнала превышает полосу частотной когерентности канала, принимаемый сигнал выражается так

}(0 = ZV-Wv/-(-W)+(0=4(0 + W ОЛ / = 1,2, (14.5.11)

к- I

где ::(/)-комплексный белый гауссовский шумовой процесс с нулевым средним. Предположим на время, что веса канальных ячеек известны. Тогда оптимальный приёмник состоит из двух фильтров, согласованных с и,(/) и из(/), за ними следуют стробирующие устройства и блок решения, который выбирает сигнал, соответствующий наибольшему выходу. Эквивалентный оптимальный приёмник использует взаимную коррекцию вместо согласованной фильтрации. В любом случае величины для решения при когерентном детектировании двоичных сигналов выражаются так

AW = 1,2 (14.5.12)

Рис. 14.5.2 иллюстрирует операции, выполняемые при расчёте величин для решения. В этой реализации оптимального приёмника два опорных сигнала задерживаются и коррелируются с принимаемым сигналом /;(/).

Альтернативная реализация оптимального приёмника сводится к использованию единственной линии задержки через которую пропускается принимаемый сигнал /}(/). В

каждом отводе этот сигнал коррелируется с c{t)s,„{t), где k = \,2,...,L и /и = 1,2. Структура приёмника показана на рис. 14.5.3. По своему действию приёмник с линией задержки пытается собрать энергию сигнала со всех принимаемых сигнальных путей, которые находятся в области линии задержки и несут одинаковую информацию.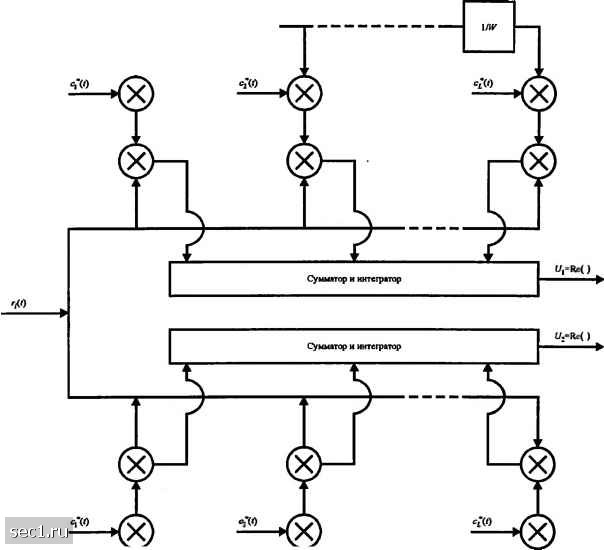

Рис. 14.S.2. Оптимальный демодулятор дпя широкополосных двоичных сигаалов (конфигурация с задержкой эталонно1х> сигнала)

Его действие в определённой степени аналогично обычным садовым граблям (гаке) и поэтому имя "RAKE-приёмник" было предложено для этой структуры приёмника Прайсом и Грином (1958).

14.5.3. Качество RAKE приёмника

Теперь рассчитаем качество RAKE приёмника при условии, что замирания сигналов достаточно медленные и позволяют оценить с(/) точно (без шума). Далее, на сигнальном

интервале c{t) считается константой и обозначается с.. Таким образом, величины для решения в (14.5.12) можно выразить в виде:

6„=Re

i:<\l{t)si{t-kiw)dt

Lit=l

/w = l, 2. (14.5.13)

Принятый сигнал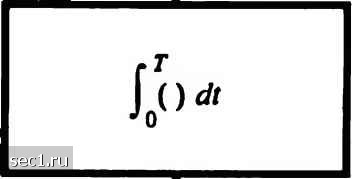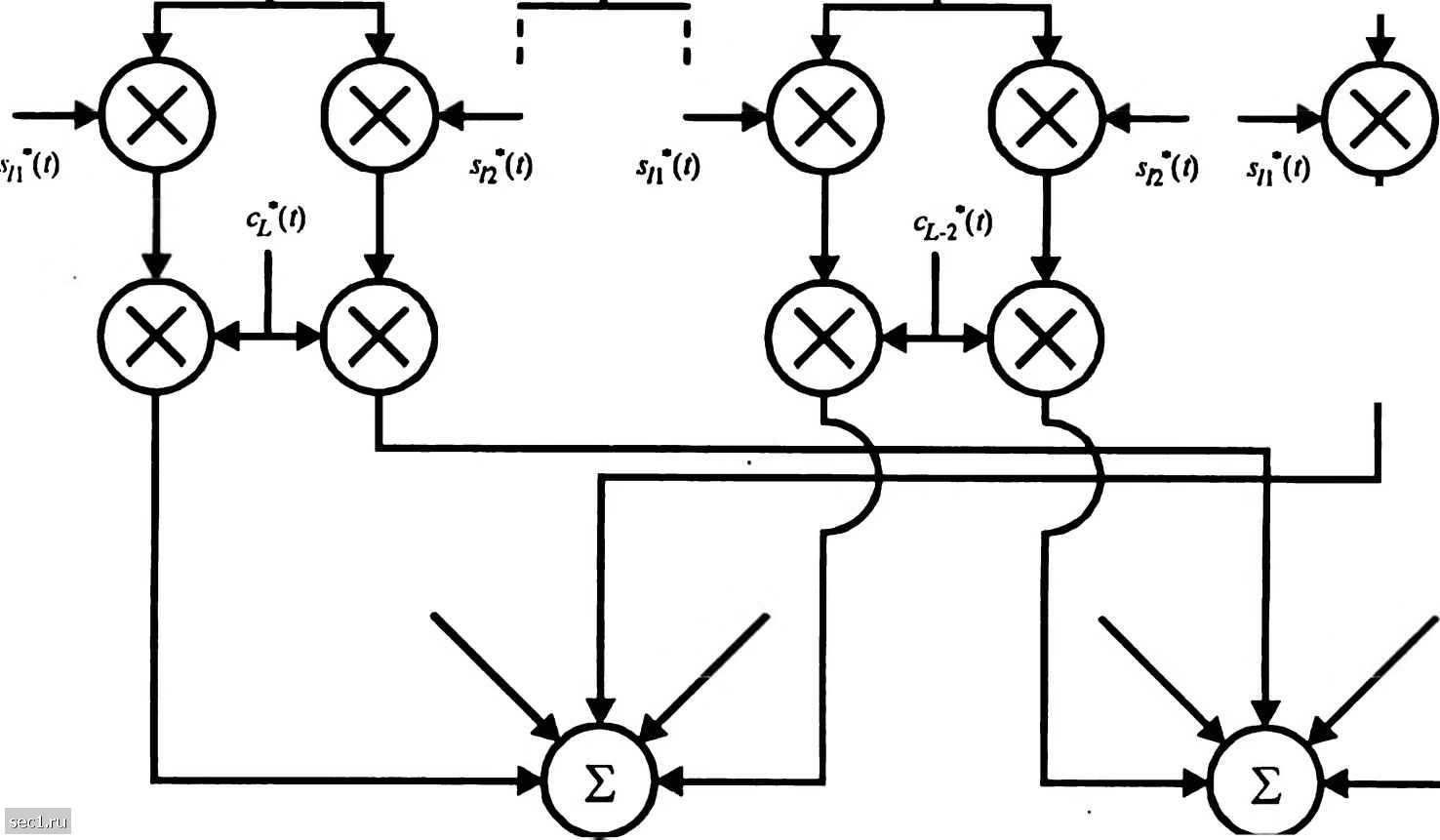

К решающей схеме

Рис. 14.5.3. Оптимальный демодулятор для широкополосных двоичных сигналов

(конфигурация с задержкой принятого сигнала)