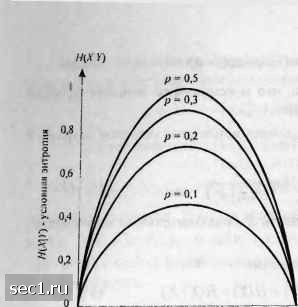о 0,2 0,4 0,6 0,8 1

1/ - всроя! iiocib символа Л" - О

Рис. 3.2.2. Условная энтропия для двоичного симметричного канала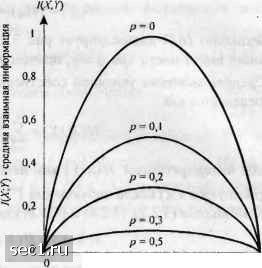

0,2 0,4 0,6 0,8 I q - всроятиосп. символа .V - О

Рис.3.2.3. Средняя взаимная информация для двоичного симметричного канала

Когда условную энтропию я(ху) рассматривают применительно к каналу с входом X и выходом у, то я(Ау) называют ненадёжностью канала на символ и её интерпретируют

как величину средней неопределённости, оставшейся в Апосле наблюдения Y.

Результаты, приведённые выше, легко обобщаются на случай произвольного числа случайных величин. В частности, предположим, что мы имеем блок из к случайных величин Х\Х%Хъ...Хк с совместной вероятностью P(x\J(2,...J(k)=P(x\=x\, x2=x2,...J(i!Xk). Тогда энтропия определяется как

я(x,,...,) = -;;•-:P(xx...xJlogP(x.x...xJ. (3.2.13)

Поскольку совместную вероятность Р{Х\ ,х2, .... Хк) можно выразить в виде

Р(х,х, • • xj = Р(х,)Р(х, IX,)Р(Хз I х.х,) • • Р{х, i х,х, • • • х, ,), (3.2.14)

то следует

Н(Х,Х,Х, ...Х,) = Н{Х,) + Н{Х, \Х,) + Н{Х, I ХХ,) +

к (3 2 15")

.. + Н(Х,\Х,...Х,.,) = Н(Х,\Х,Х,...Х, ,).

с учётом результата H{x)>h(x\y), rjxeX-x„, и ¥=Х\х2..Л\,.и из (3.2.15) следует

ЩХ,Х, ...X,) <fH(XJ, (3.2.16)

причём равенство имеет место тогда, и только тогда, когда случайные величины Х[,х2, ...,Xk статистически независимы.

3.2.2. Измерение информации для непрерывных случайных величин

Определение взаимной информации, данное выше для дискретных случайных величин, можно непосредственно использовать для непрерывных случайных величин. В частности.

я(у X) называют энтропией шума в канале (прп)

если X и У - случайные величины с СПВ р(х.у) и собственными ФПВ р(х) и р{у), то средняя взаимная информация между XkY определяется как

I(X,Y)= Г Г р(х)р(у IX)logf dxdy. (3.2.17) j-«> J-« p(x)piy)

Несмотря на то, что выражение для средней взаимной информации легко обобщается на непрерывные случайные величины, сделать это для собственной информации непрерывной случайной величины невозможно. Проблема в том, что непрерывные случайные величины требуют неограниченного числа двоичных цифр для их точного представления. Следовательно, энтропия непрерывной случайной величины также неограниченна. Всё же введём характеристику, которую назовём дифференциальной энтропией непрерывной случайной величины X.

КХ) = -[pix)logp(x)dx. (3.2.18)

Подчеркнём, что эта характеристика не имеет физического смысла собственной информации, хотя может показаться, что она является естественным обобщением определения энтропии для дискретной случайной величины (см. задачу 3.6). Определим среднюю условную дифференциальную энтропию X при заданном У как

hiX\Y) = -r Гpix,y)logpix\y)dxdy. (3.2.19)

• -00 J-eo

Тогда среднюю взаимную информацию можно выразить как

I(X;Y)hiX)-h(X\Y)

или альтернативно как

I(XJ) = hiY)-hiY\X). В некоторых случаях, представляющих практический интерес, случайная величина X является дискретной, а У - непрерывной. Для конкретности предположим, что X имеет возможные исходы х„ i=\, 2, п, а У определяется собственной ФПВ р(у). Если X и Y статистически взаимосвязаны, мы можем выразить р(у) так:

Взаимная информация относительно события Х~х, при наблюдении события Y=y определяется как

Тогда средняя взаимная информация между Аи У

Piy)

ИХ;У) = X Г р(у I X,)P(x,)logdy.

(3.2.20)

(3.2.21)

Пример 3.2.5. Предположим, что X является дискретной случайной величиной с двумя равновероятными выходами Xi = А н Xj =-А. Предположим, что условная ФПВ р(У,), р1,2, является гауссовской со средним X, и дисперсией ст, т.е.

Р(У\А) =

р(у\-А) =

V27ia

(3.2.22)

Средняя взаимная информация согласно (3.2.21) равна KX;Y)\l

Piy\A)\ogP.py\-A)\og-Py-

Piy)

Piy) J

(3.2.23)

Р(У) = i [Р(У I А) + р{у I -А)]. (3.2.24)

В гл. 7 мы покажем, что средняя взаимная информация HX;Y), определяемая (3.2.23), представляет пропускную способность канала с двоичным входом и аддитивным гауссовским шумом.

3.3. КОДИРОВАНИЕ ДЛЯ ДИСКРЕТНЫХ ИСТОЧНИКОВ

в разд. 3.2 мы ввели меру для информационного содержания дискретной случайной величины X. Когда X является выходом дискретного источника, энтропия Н{Х) источника определяет среднее количество информации на символ, выдаваемой источником. В этом разделе мы рассмотрим процесс кодирования выхода источника, т.е. процесс представления выхода источника последовательностью двоичных цифр. Эффективность способа кодирования источника можно измерить путём сравнения среднего количества двоичных символов кодера на один символ источника и энтропии источника Н{Х).

На первый взгляд может показаться, что кодирование дискретного источника с конечным объёмом алфавита является простой проблемой. Однако это верно, только если источник без памяти, т.е. когда последовательные символы источника статистически независимы и каждый символ кодируется отдельно. Дискретный источник без памяти СДИБП) является простейшей моделью, которую можно предложить для физического источника. Эта идеализированная математическая модель подходит для немногих физических источников. Например, можно легко убедиться в том, что последовательно выдаваемые буквы устройством, печатающим осмысленный текст, статистически взаимосвязаны. С другой стороны, если печатается компьютерная программа на языке Фортран, то можно ожидать, что зависимость в последовательности выходных символов проявится значительно меньше. Во всяком случае, мы покажем, что всегда более эффективно кодировать блок символов источника вместо того, чтобы кодировать каждый символ отдельно. Если размер блока достаточно большой, то среднее количество символов кодера на один выходной символ источника можно сделать сколь угодно близким к энтропии источника.

3.3.1. Кодирование для дискретных источников без памяти

Предположим, что ДИБП выдает буквы или символы каждые т, секунд. Каждый

символ выбирается из конечного алфавита х„2,Z,, с вероятностью Р(х,), /=1. 2,..., Энтропия ДИБП в битах на символ

Н{Х) = -Y,P{x,)\og, Р{х,) < log, L. (3.3.1)

причем равенство имеет место, если все символы равновероятны. Н{Х) определяет среднее число бит на символ источника, а производительность источника в битах/с определяется как Н(Х)/т .

Кодовые слова фиксированной длины. Сначала рассмотрим схему блокового кодирования, которая сопоставляет уникальный ряд из R двоичных символов с каждым символом источника. Поскольку имеется L возможных символов источника, то число двоичных символов кодера на один символ источника при уникальном кодировании

i2 = log,Z, (3.3.2)

когда L равно целой степени основания 2, и

R\\og,L\+\, (3.3.3)

когда L не равно целой степени основания 2.